勝負のやめ時

収束はするけれど

• こちらでサイコロを使った勝負について扱っている
• シミュレーションしているので、二項分布を使った確率計算にしてみる
• トータルで勝つ確率は、試行数を増やすと、大まかには上って行く
• ただし、上がっては下がり、の繰り返し
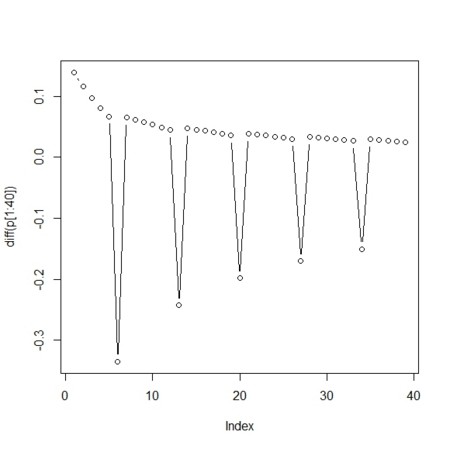
• 周期は「６回」であることも図示できる

# サイコロを振る回数
n <- 1:1000
# 得点の期待値
v <- rep(0,length(n))
# トータルで勝つ確率と、個々の試行で勝つ回数別に計算した確率の和(検算用)
p <- q <- v
# サイコロを振る回数ごとにループ
for(i in 1:length(v)){
# 個々のサイコロ振りで勝つ回数
	t <- 0:n[i]
# 同、負ける回数
	s <- n[i]:0
# トータルのコスト
	lose <- n[i]
# 勝つ回数別の得点
	gain <- t * 7
# トータルで勝つ場合の「個々のサイコロ振りで勝つ回数」のベクトル。また、その場合の負ける回数のベクトル
	win <- which(gain-lose > 0)
	#print(win)
	win.t <- t[win]
	win.s <- s[win]
# 計算しよう	
	v[i] <- -n[i] + sum(exp(lgamma(n[i] + 1) - lgamma(t+1) - lgamma(n[i]-t+1) + s * log(5)  -(n[i]) * log(6) + log(7)+log(t)))
	
	p[i] <- sum(exp(lgamma(n[i] + 1) - lgamma(win.t+1) - lgamma(n[i]-win.t+1) + win.s * log(5)  -(n[i]) * log(6) ))
	q[i] <- sum(exp(lgamma(n[i] + 1) - lgamma(t+1) - lgamma(n[i]-t+1) + s * log(5)  -(n[i]) * log(6)))
}
# プロットしよう
plot(n,v)
# 周期的変化をする
plot(n,p)
# 検算結果をプロットしよう
plot(n,q)
# 「トータルで勝つ確率の増分をプロットすることで、周期的変化の「周期」を確認しよう
plot(diff(p[1:40]),type="b")