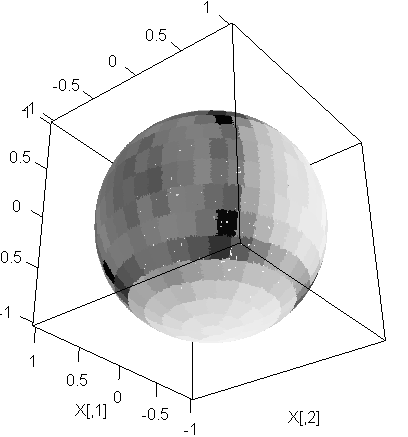2012-07-29

角座標的度数分布、タイリング

ryamada2012-07-29

2012-07-29

球面配置

度数分布角座標円球

昨日は球の分裂からの派生で円形・球面の度数分布について書いた
そのとき、半径の広がりに応じて、指数関数的にセルを増やすことにしたのだが、よく考えたら、それは変
タイリングなので、正六角形の埋め尽くし、とかが適当。球面なら、サッカーボール型か
正六角形タイル座標を決めたり(こちら)や、サッカーボールの座標を決めたり(こちら)とかでもよいが…
- 切頂十二面体とか、polyhedra一般とか、コクセター記法とか…(深入りしすぎないようにしたい)polyhedra_coordinate、truncated_icosahedronとか
タイルの数だけを参考にして、角座標で扇形に指定する方がやっぱり簡単か…
正六角形タイリングに模して、3次元球面を1,6,12,18と覆うとすると

Sphere.Histogram.3.2 <- function(X,ts,k){
	ts.2 <- c(ts,ts[length(ts):1])
	cum.ts <- cumsum(ts)
	max.cum.ts <- cum.ts[length(cum.ts)]
	phis <- c(0,acos(1-cum.ts/max.cum.ts))
	diff.phis <- diff(phis)
	phis <- c(phis[-length(phis)],cumsum(c(phis[length(phis)],diff.phis[length(diff.phis):1])))
	#print(r)
	Hist <- list()
	
	thetas <- list()
	for(i in 1:k){
		thetas[[i]] <- seq(from = 0, to = 2*pi, length =ts[i]+1)
		Hist[[i]] <- rep(0,length(thetas[[i]]-1))
	}
	tmpks <- k:1
	for(i in 1:length(tmpks)){
		thetas[[k+i]] <- thetas[[k+1-i]]
		Hist[[k+i]] <- Hist[[k+1-i]]
	}
	print(thetas)
	Cmpx <- complex(real = X[,1],imaginary = X[,2])
	Md <- acos(X[,3])
	#Md <- Mod(Cmpx)
	Ag <- Arg(Cmpx)
	neg <- which(Ag < 0)
	Ag[neg] <- 2*pi +Ag[neg]
	for(i in 1:length(Hist)){
		s <- which(Md >= phis[i] & Md < phis[i+1])
		a <- Ag[s] %/% (thetas[[i]][2]) +1
		#print(i)
		print(range(Ag[s]))
		print(a)
		Hist[[i]] <- tabulate(a,nbins = ts.2[i]+1)
		#if(i<=k){
		#	Hist[[i]] <- tabulate(a,nbins = ts[i]+1)
		#}else{
		#	Hist[[i]] <- tabulate(a,nbins = ts[k+(ts[i]-k]+1)
		#}
		Hist[[i]] <- Hist[[i]][-length(Hist[[i]])]
	}
	return(list(Hist=Hist,X=X,Md=Md,Ag=Ag,t=t,k=k,phis=phis,thetas=thetas))
}
n.pt <- 100000

X <- matrix(rnorm(n.pt*3),ncol=3)
X <- X/sqrt(apply(X^2,1,sum))
#apply(X^2,1,sum)

#X <- X[which(X[,3]>=0),]

R <- sqrt(X[,1]^2+X[,2]^2)

the <- asin(R)

t <- seq(from=0,to=pi/2,length=100)

L <- rep(0,length(t))
for(i in 1:length(t)){
	L[i] <- length(which(R <= sin(t[i])))
}

plot(t,L)

ts <- c(1,6,12,18)
sp.out3.2 <- Sphere.Histogram.3.2(X,ts,4)
sp.out3.2$Hist

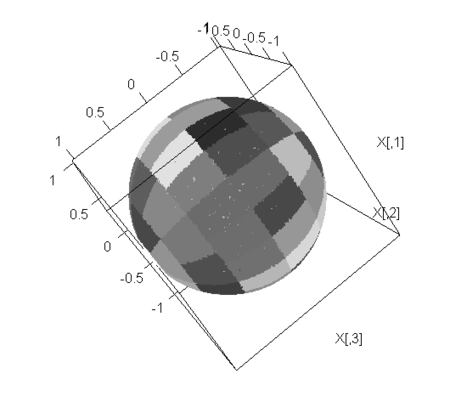
プロットするには
- 得られたタイル別の度数を引数として渡しつつ、タイルのエリア情報を渡し、そこに乱点で色を付ける、ということでやってみよう

plot.SphereHist <- function(sp.out,ts,k,n=100000){
	n.pt <- n
	phis <- sp.out$phis
	thetas <- sp.out$thetas
	X <- matrix(rnorm(n.pt*3),ncol=3)
	X <- X/sqrt(apply(X^2,1,sum))
	Cmpx <- complex(real = X[,1],imaginary = X[,2])
	Md <- acos(X[,3])
	#Md <- Mod(Cmpx)
	Ag <- Arg(Cmpx)
	neg <- which(Ag < 0)
	Ag[neg] <- 2*pi +Ag[neg]
	cols <- rep(0,length(X[,1]))
	for(i in 1:length(sp.out$Hist)){
		s <- which(Md >= phis[i] & Md < phis[i+1])
		a <- Ag[s] %/% (thetas[[i]][2]) +1
		cols[s] <- sp.out$Hist[[i]][a]
	}
	library(rgl)
	plot3d(X,col = gray((max(cols)-cols)/(max(cols)-min(cols))),cex=0.1)
}

plot.SphereHist(sp.out3.2,ts,k)

まだらにしてみよう

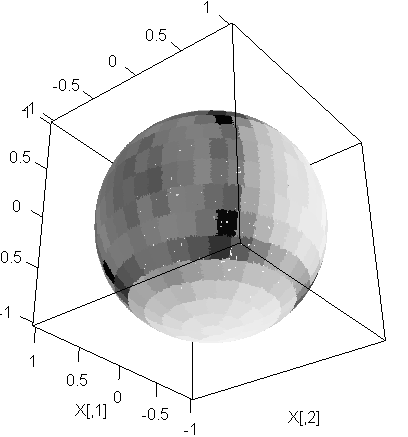
n.pt <- 100000

X <- matrix(rnorm(n.pt*3),ncol=3)
X[,1] <- X[,1] +1
tmp.X <- matrix(rnorm(n.pt*3),ncol=3)
tmp.X[,1] <- cos(tmp.X[,1]*8+pi/3)
tmp.X[,2] <- sin(tmp.X[,2]*10)
tmp.X[,3] <- cos(tmp.X[,3]*10)
X <- rbind(X,tmp.X)
X <- X/sqrt(apply(X^2,1,sum))
#apply(X^2,1,sum)

#X <- X[which(X[,3]>=0),]

R <- sqrt(X[,1]^2+X[,2]^2)

the <- asin(R)

t <- seq(from=0,to=pi/2,length=100)

L <- rep(0,length(t))
for(i in 1:length(t)){
	L[i] <- length(which(R <= sin(t[i])))
}

plot(t,L)

t.len <- 8
ts <- c(1,6*(1:t.len))
k <- length(ts)
sp.out3.2 <- Sphere.Histogram.3.2(X,ts,k)
sp.out3.2$Hist

plot.SphereHist <- function(sp.out,ts,k,n=100000){
	n.pt <- n
	phis <- sp.out$phis
	thetas <- sp.out$thetas
	X <- matrix(rnorm(n.pt*3),ncol=3)
	X <- X/sqrt(apply(X^2,1,sum))
	Cmpx <- complex(real = X[,1],imaginary = X[,2])
	Md <- acos(X[,3])
	#Md <- Mod(Cmpx)
	Ag <- Arg(Cmpx)
	neg <- which(Ag < 0)
	Ag[neg] <- 2*pi +Ag[neg]
	cols <- rep(0,length(X[,1]))
	for(i in 1:length(sp.out$Hist)){
		s <- which(Md >= phis[i] & Md < phis[i+1])
		a <- Ag[s] %/% (thetas[[i]][2]) +1
		cols[s] <- sp.out$Hist[[i]][a]
	}
	library(rgl)
	plot3d(X,col = gray((max(cols)-cols)/(max(cols)-min(cols))),cex=0.1)
}

plot.SphereHist(sp.out3.2,ts,k)