arxiv.org
- n個の点が円周上に配置されているとする
- その内部円板に有向グラフがあるとき、適当な変形を加えることで、3-valent有向グラフに変えることができる
- このグラフをplanar circular directed graphと呼ぶ
- さらに、3-valent有向グラフを3-valent bipartite plabic グラフに変えることもできる
- このplanar circular directed graphの円周上の点はただ１本の辺に接続するというルールがあるので、すべての円周上の点は、湧き出し口か吸い込み口かのどちらかになる
- 今、湧き出し口の数がk個、吸い込み口の数がn-k個であり、円周上の点の数がnであるとする
- このグラフに
行列を定義することができる。Boundary measurement matrixと呼ぶ
- この行列は
であるので、この行列には、Plucker座標が定められる
- ちなみに、Plucker座標とは、
からk個の要素を取り出したときに(
通りの組合せが作れる)、それぞれの組について、Boundary measurement matrixの該当列を取り出すことで、
行列が取れるが、その行列の行列式の値を取り出すことで、結局、個の値が取れることとなり、その値を並べたものがPlucker 座標であり、グラスマニアンという空間上の点を指し示している(ただし、斉次座標になっている)
- さて、planar circular directed graphの場合に、Boundary measurement matrix (
の要素
として、湧き出し口頂点から１頂点 i を取り除き、その代わりに吸い込み口の頂点から１頂点 jを追加してできるk個の頂点の組合せを考えた時に、頂点iから湧き出して、頂点jに吸い込まれるようなパスの本数に相当する値
を考え、j番目が、湧き出し口のすべてより若いか、すべてより大きいか、湧き出し口の間に挟まれているか、さらには気にしている湧き出し口頂点 i番と比べて若いか大きいかによって、の符号を変えたものをとすることにする
- このとき、Plucker 座標の要素のすべてが非負になることが知られている
- その結果、planar circular networkはpositive grassmanian上の点に対応付けられる、という話がある
- このリンク先のペイパーでは、このPlucker座標が、k個の列の選び方に応じて、networkに取れる、ある種の正エッジ重みづけパス本数セットに関する値になっていることを示している
- 基本的には、正重みづけでの「取りうるパスの場合」に関する足し合わせであることから、すべてのPlucker座標が非負になる
- また、そのパス本数セットに相当する値の計算式は、内部にサイクルがなければ単純な式になり、サイクルがあると、有理式になるのだが、その様子が団代数・団変数と同じ挙動をすることも示せる
- そもそも、planar circular networkで小行列式が非交叉パスの取り方の場合分けと関係した非負の値がとれる(ただし、符号の考慮が必要)な話は、左列にあるn頂点から、右列にあるn頂点へのplanar directed graphがあったときに、非交叉パスの場合の数が符号を考えなくて良い小行列式で表されることが知られており、それをcircularに拡張した時に、湧き出し口・吸い込み口の相互位置関係に関して複雑になっている部分を符号操作で一般化したものになっている
- 内部のサイクルによる補正のことは忘れて、あるplanar circular networkがあって、そのBoundary measurement matrixを取り、そのPlucker 座標がすべて正になることを例で確かめてみよう
- こんなグラフ
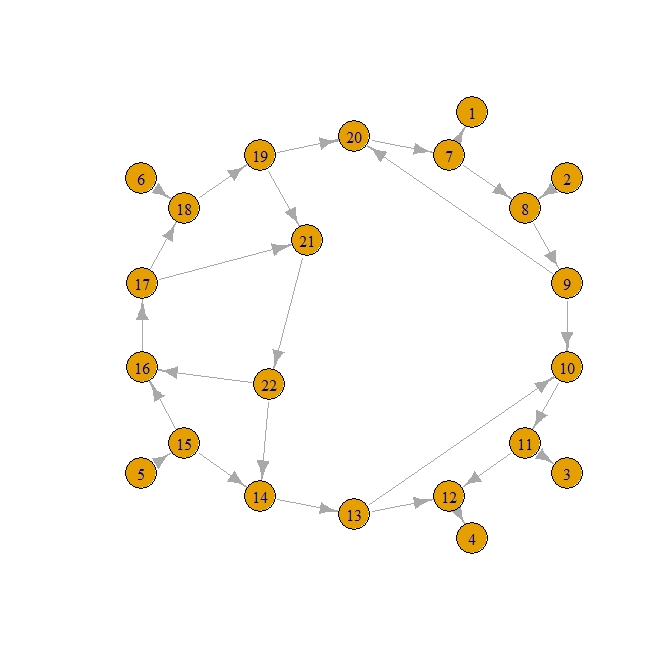
tmp <- c(7,1,2,8,11,3,12,4,5,15,6,18,7,8,8,9,9,10,10,11,11,12,13,12,14,13,15,14,15,16,16,17,17,18,18,19,19,20,20,7,9,20,13,10,19,21,21,22,22,14,22,16,17,21)
el <- matrix(tmp,byrow=TRUE,ncol=2)
library(igraph)
g <- graph.edgelist(el)
theta <- pi/2 - (1:14)/14 * 2 * pi
theta. <- theta[c(1,2,5,6,9,12,1:14,13,9)]
r <- c(rep(1,6),rep(0.8,14),rep(0.4,2))
coords <- cbind(cos(theta.),sin(theta.)) * r
plot(g,layout = coords)
- 湧き出し口頂点は2,5,6で、吸い込み口頂点は1,3,4
- このBoundary measurement matrixは以下のようになる
paths <- list()
for(i in 1:22){
paths[[i]] <- list()
for(j in 1:22){
paths[[i]][[j]] <- all_simple_paths(g,i,j)
}
}
A <- matrix(0,3,6)
sources <- c(2,5,6)
for(i in 1:3){
for(j in 1:6){
A[i,j] <- length(paths[[sources[i]]][[j]])
btwn <- which((j-sources) * (sources[i] - sources) < 0)
tmp.sign <- (-1)^length(btwn)
A[i,j] <- A[i,j] * tmp.sign
if(sources[i] == j){
A[i,j] <- 1
}
}
}
> A
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 1 1 1 1 0 0
[2,] -1 0 4 7 1 0
[3,] 1 0 -2 -3 0 1
-
- 1,2,3行目はそれぞれ、2,5,6湧き出し頂点に対応する
- 1行目は、2番頂点から、1,2,3,4,5,6頂点へのパスの場合の数。2と1,2,3,4,5,6の間には、湧き出し口が挟まれていないので、すべての値が正。湧き出し口5,6へのパスはなく、自身へのパスの数は1
- 2行目は、5番頂点から、1,2,3,4,5,6頂点のパスの場合の数。5と1の間には湧き出し口2(１個、奇数個)あるので、負。2,3,45,6と5の間には湧き出し口はないので正
- 3行目は、6番頂点から、1,2,3,4,5,6頂点のパスの場合の数。6と1の間には湧き出し口2,5(２個、偶数個)あるので、正。2,3,4と6の間には、湧き出し口5(1個、奇数個)あるので負(ただし、0は0）
- すべての組合せについて小行列式を計算して表示してみると正になっている
library(gtools)
cmb <- combinations(6,3)
for(i in 1:length(cmb[,1])){
print("cmb")
print(cmb[i,])
print(det(A[,cmb[i,]]))
}
> for(i in 1:length(cmb[,1])){
+ print("cmb")
+ print(cmb[i,])
+ print(det(A[,cmb[i,]]))
+ }
[1] "cmb"
[1] 1 2 3
[1] 2
[1] "cmb"
[1] 1 2 4
[1] 4
[1] "cmb"
[1] 1 2 5
[1] 1
[1] "cmb"
[1] 1 2 6
[1] 1
[1] "cmb"
[1] 1 3 4
[1] 4
[1] "cmb"
[1] 1 3 5
[1] 3
[1] "cmb"
[1] 1 3 6
[1] 5
[1] "cmb"
[1] 1 4 5
[1] 4
[1] "cmb"
[1] 1 4 6
[1] 8
[1] "cmb"
[1] 1 5 6
[1] 1
[1] "cmb"
[1] 2 3 4
[1] 2
[1] "cmb"
[1] 2 3 5
[1] 2
[1] "cmb"
[1] 2 3 6
[1] 4
[1] "cmb"
[1] 2 4 5
[1] 3
[1] "cmb"
[1] 2 4 6
[1] 7
[1] "cmb"
[1] 2 5 6
[1] 1
[1] "cmb"
[1] 3 4 5
[1] 1
[1] "cmb"
[1] 3 4 6
[1] 3
[1] "cmb"
[1] 3 5 6
[1] 1
[1] "cmb"
[1] 4 5 6
[1] 1
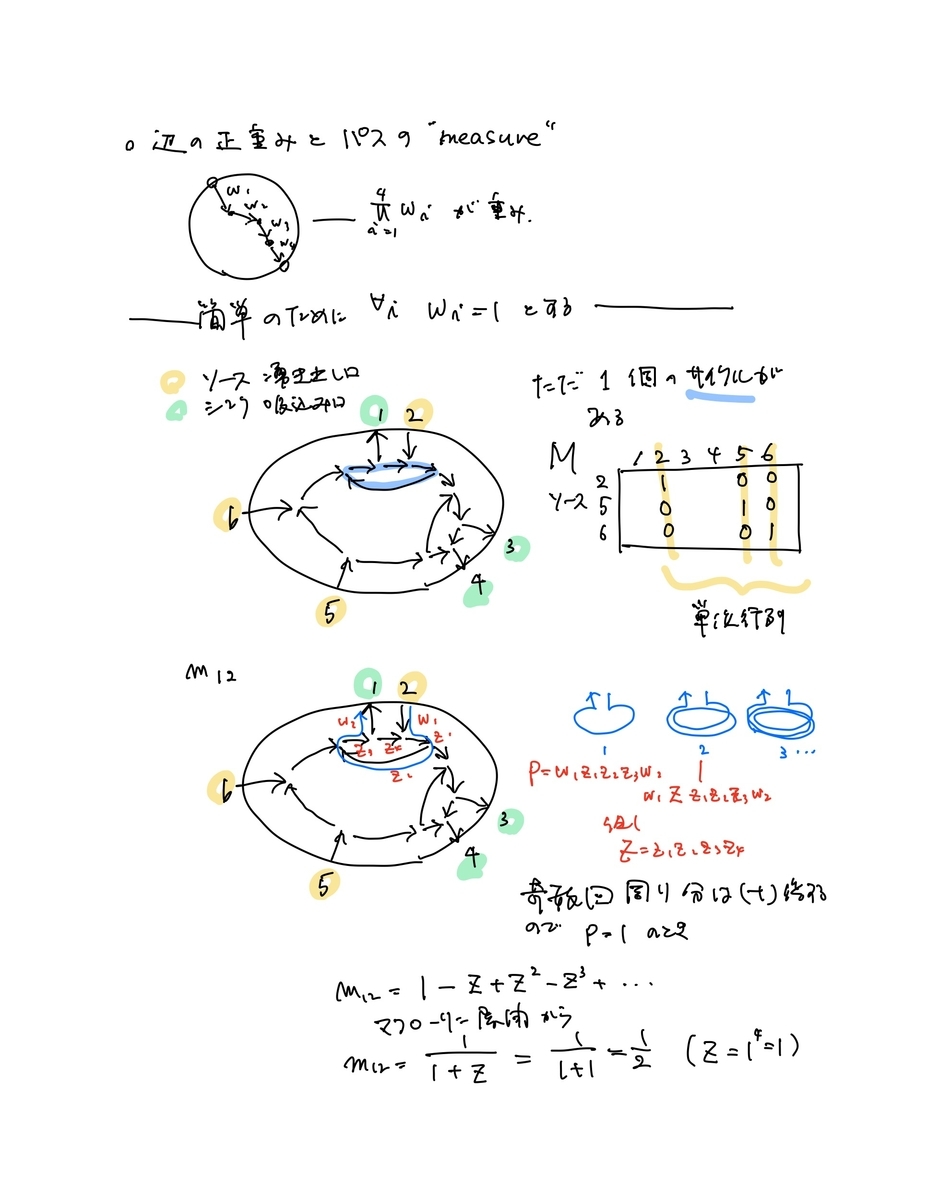
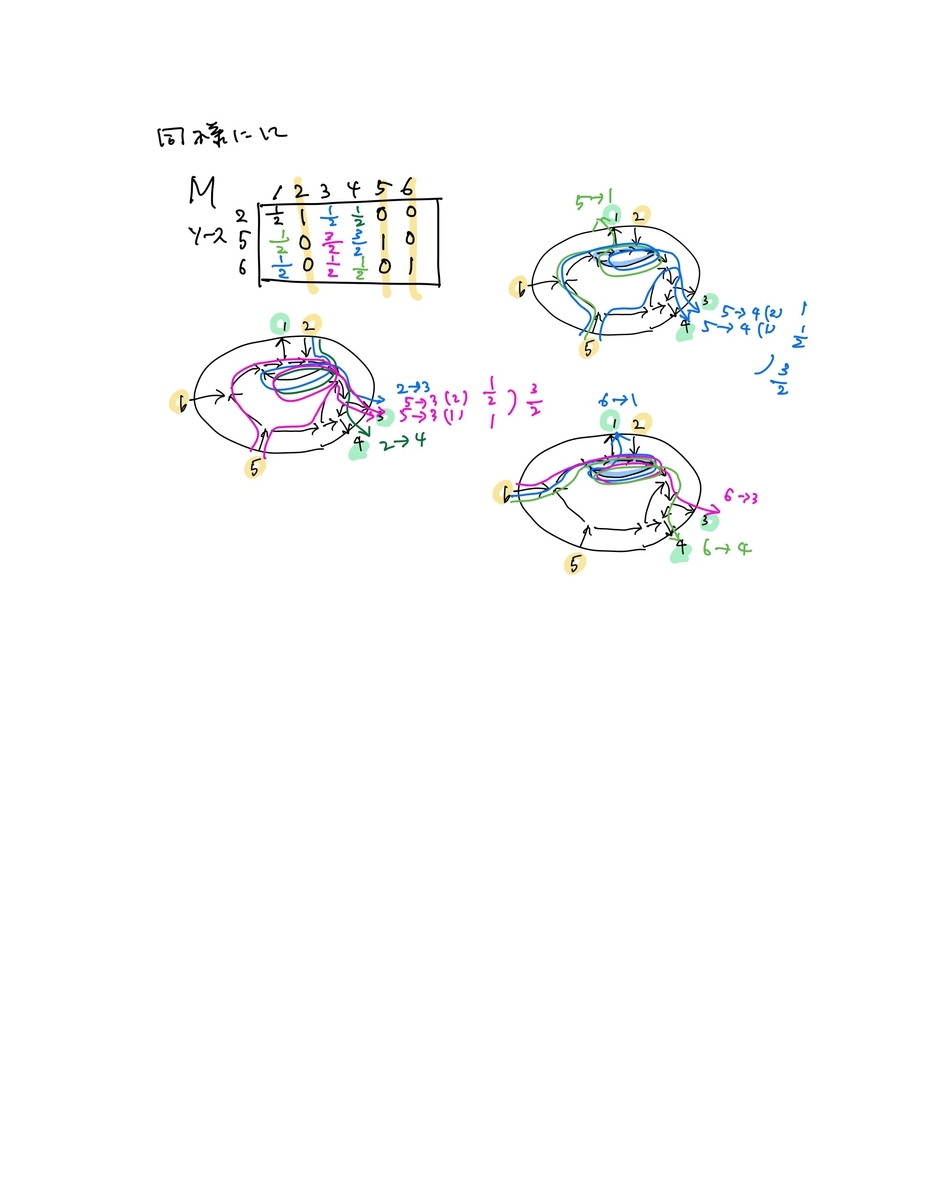
- この行列Mに、頂点ペア間のソース頂点数で符号をつけ、Plucker座標を計算すると、すべて非負
- このPlucker座標(小行列式)は、符号を変える前のMの要素を使って、ソースから行先頂点への矢印の交叉の有無・交叉の数を考慮した式でも計算できることが示せる
D <- matrix(c(1/2,1,1/2,1/2,0,0,1/2,0,3/2,3/2,1,0,1/2,0,1/2,1/2,0,1),byrow=TRUE,ncol=6)
D2 <- D * sign(A)
library(gtools)
cmb <- combinations(6,3)
for(i in 1:length(cmb[,1])){
print("cmb")
print(cmb[i,])
print(det(D[,cmb[i,]]))
}
> D <- matrix(c(1/2,1,1/2,1/2,0,0,1/2,0,3/2,3/2,1,0,1/2,0,1/2,1/2,0,1),byrow=TRUE,ncol=6)
> D[1,2] <- D[2,5] <- D[3,6] <- 1
> D2 <- D * sign(A)
>
> library(gtools)
> cmb <- combinations(6,3)
> for(i in 1:length(cmb[,1])){
+ print("cmb")
+ print(cmb[i,])
+ print(det(D2[,cmb[i,]]))
+ }
[1] "cmb"
[1] 1 2 3
[1] 0.5
[1] "cmb"
[1] 1 2 4
[1] 0.5
[1] "cmb"
[1] 1 2 5
[1] 0.5
[1] "cmb"
[1] 1 2 6
[1] 0.5
[1] "cmb"
[1] 1 3 4
[1] 0
[1] "cmb"
[1] 1 3 5
[1] 0.5
[1] "cmb"
[1] 1 3 6
[1] 1
[1] "cmb"
[1] 1 4 5
[1] 0.5
[1] "cmb"
[1] 1 4 6
[1] 1
[1] "cmb"
[1] 1 5 6
[1] 0.5
[1] "cmb"
[1] 2 3 4
[1] 0
[1] "cmb"
[1] 2 3 5
[1] 0.5
[1] "cmb"
[1] 2 3 6
[1] 1.5
[1] "cmb"
[1] 2 4 5
[1] 0.5
[1] "cmb"
[1] 2 4 6
[1] 1.5
[1] "cmb"
[1] 2 5 6
[1] 1
[1] "cmb"
[1] 3 4 5
[1] 0
[1] "cmb"
[1] 3 4 6
[1] 0
[1] "cmb"
[1] 3 5 6
[1] 0.5
[1] "cmb"
[1] 4 5 6
[1] 0.5
