木グラフの流量計算

• 木グラフがあって、そこに確率質量分布があるとする
• 木グラフは不変で、別の確率質量分布に変化したとする
• どのエッジをどれだけのフローがあったかを計算するには、エッジ数ｘエッジ数(ノード数ー１の二乗)の正方行列を用いた連立方程式の解で出す

library(igraph)
n.v <- 15
g <- graph.tree(n.v, 2,mode="out")
plot(g,layout=layout.kamada.kawai)
el <- get.edgelist(g)
w.v.1 <- runif(n.v)
w.v.1 <- w.v.1/sum(w.v.1)

w.v.2 <- runif(n.v) + w.v.1*5
w.v.2 <- w.v.2/sum(w.v.2)

w.diff <- w.v.2 - w.v.1
w.diff.abs <- abs(w.diff)

k.size <- 50/max(c(w.v.1,w.v.2,w.diff.abs))
par(mfrow=c(2,2))
lay <- layout.kamada.kawai(g)
plot(g,layout=lay,vertex.size=w.v.1*k.size)
plot(g,layout=lay,vertex.size=w.v.2*k.size)
# Increased vertices are blue
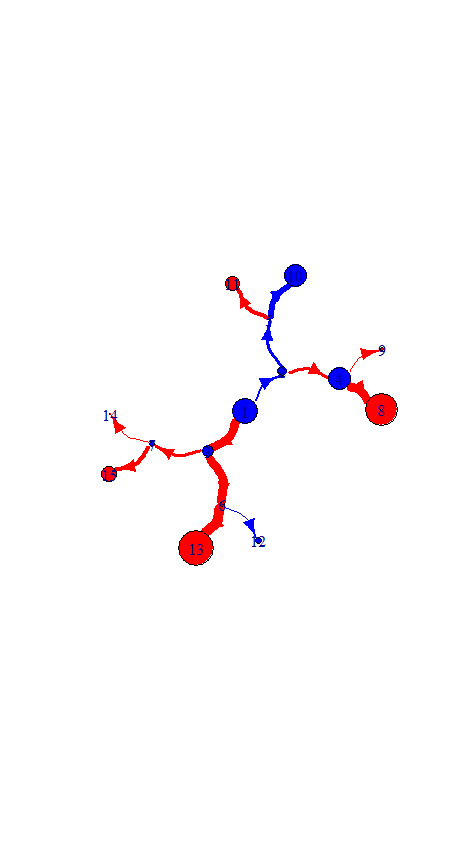
plot(g,layout=lay,vertex.size=w.diff.abs*k.size,vertex.color=sign(w.diff)+3)
par(mfrow=c(1,1))
n.e <- length(el[,1])
X <- matrix(0,length(V(g)),n.e)
for(i in 1:n.e){
  X[el[i,1],i] <- -1
	X[el[i,2],i] <- 1
}
X
f <- solve(X[1:n.e,],w.diff[1:n.e])
f
# 検算
X %*% f - w.diff
k.e.width <- 10/max(abs(f))
plot(g,layout=lay,vertex.size=w.diff.abs*k.size,vertex.color=sign(w.diff)+3,edge.width=abs(f)*k.e.width,edge.color = sign(f)+3,edge.curved=TRUE)