2014-01-23

配偶者を取り換える

MIKU R 順列マッチング

昨日のMIKUでマッチングと、その「安定な状態」という話を聞いた
安定結婚問題と言うものがあるらしい
安定結婚問題の本当の定義をしっかり確認していないのだけれど、次のような問題設定ができるようだ(その問題設定が安定結婚なのか、それとは違うのか、を確認していない、と言うことなのだが)
(簡単のために)、男女が同数 $Nm=Nf$ いるとする
すべての男は、すべての女に同順位なしの順序をつけ
すべての女は、すべての男に、同様に同順位なしの順位をつける
ここまでで、 $Nm \times Nm$ の行列が２つできた
ここで、すべてのマッチング(Nm x 2人からNmの男女ペアを作ること)の場合を考える
その場合の数は $Nm!$
マッチングには「多くの人が満足」な場合と「そうでない場合」とがある
今、あるマッチングが出来上がったときに、２組の夫婦は出会って、「取り換えない？」と相談するかもしれないという
そのとき、その２組の夫婦のみに着目すると、２人の男と２人の女の計４人がいる
その４人で、男女のペアは４つできる。そして、あるマッチングの状態だと「夫婦となっているペア」が２つあり、「夫婦でないペア」が２つある
今、「夫婦になっていないペア」２組のうち、どちらか１組でも、男女の両人が「今の結婚状態よりも、「不倫した方がよい」〜「離婚して再婚した方がよい」と考えるとき、夫婦の組み換えが起きる、と仮定する(それによって、幸せになる２人は必ずいるが、残りの２人が幸せになるかどうかは、今は、気にしないとする)
そんな状態をグラフで表してみたい
$Nm!$ 通りのマッチングを $1,2,...,Nm$ の順列に対応付け、それをグラフのノードとする
この $Nm!$ 個のノードのうち、２ペア(4人)だけが違うような順列２つについては、「不倫、離婚＆再婚」ルールで入れ替えるアクションが起きうるとして、その２順列に有向エッジを引くとする
以下は、そんな絵を描くソース
1つには、２ペアのみが違う順列間にエッジを渡したグラフ(これはPermutohedron)
もう一つが、「不倫、離婚・再婚」グラフ

# 男女の人数
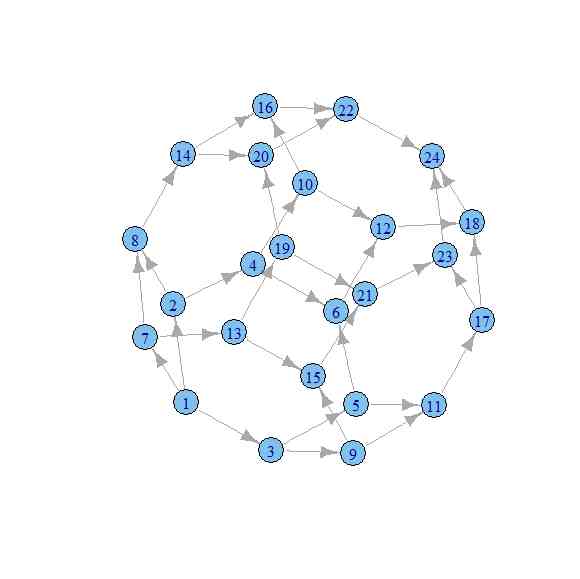
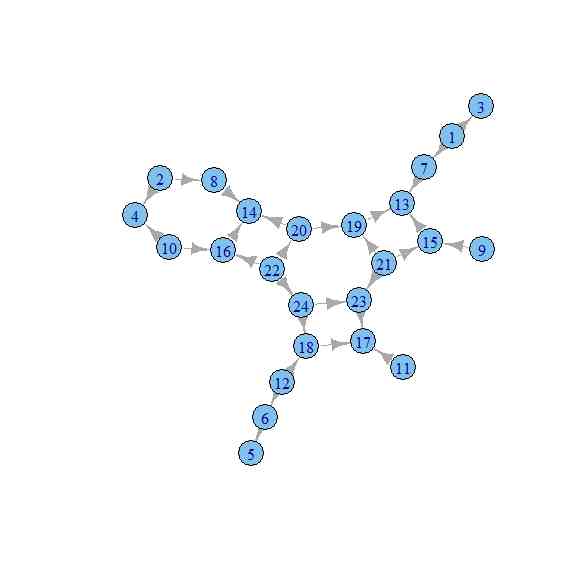
Nm <- 4
Nf <- Nm
# 好み行列。男が女につけた好みと女が男につけた好み
Mm <- matrix(0,Nm,Nf)
Mf <- matrix(0,Nf,Nm)
for(i in 1:Nm){
	Mm[i,] <- sample(1:Nf)
}
for(i in 1:Nf){
	Mf[i,] <- sample(1:Nm)
}

library(gtools)
my.stable.marriage <- function(Mm,Mf){
# 男女人数
	Nm <- length(Mm[,1])
	Nf <- length(Mm[1,])
# 全順列を列挙
	p <- permutations(Nm,Nm)
# 順列の総数
	n.s <- length(p[,1])
# 2ペアのみが違う順列間にエッジを引く場合のエッジリスト
	el.list <- matrix(0,0,2)
# 不倫ルールで交換が起きる場合のエッジリスト
	el.list.2 <- el.list
# すべての順列２つを比較
	for(i in 1:(n.s-1)){
		for(j in (i+1):n.s){
# 2か所だけ違う場合を取り出す
			if(sum(abs(p[i,]-p[j,]))==2){
				el.list <- rbind(el.list,c(i,j))
# 取り換える男２人を取り出す
				swap <- which(p[i,]-p[j,]!=0)
				M1 <- swap[1]
				M2 <- swap[2]
# 対応する女を順列i ,順列 jのそれぞれで取り出す
				F1.i <- p[i,swap[1]]
				F2.i <- p[i,swap[2]]
				F1.j <- p[j,swap[1]]
				F2.j <- p[j,swap[2]]
# iのとき、jのときのそれぞれの、配偶者の「好みの順位」を取り出す
				# i
				order.m_f1i <- which(Mm[M1,]==F1.i)
				order.f_m1i <- which(Mf[F1.i,]==M1)
				
				order.m_f2i <- which(Mm[M2,]==F2.i)
				order.f_m2i <- which(Mf[F2.i,]==M2)
				# j
				order.m_f1j <- which(Mm[M1,]==F1.j)
				order.f_m1j <- which(Mf[F1.j,]==M1)
				
				order.m_f2j <- which(Mm[M2,]==F2.j)
				order.f_m2j <- which(Mf[F2.j,]==M2)

# 不倫が成立するかどうかの判定はこんな感じ？				
				if((order.m_f1i - order.m_f1j) * (order.f_m1i - order.f_m1j) >0){
					if((order.m_f1i -order.m_f1j)>0){
						el.list.2 <- rbind(el.list.2,c(i,j))
					}else{
						el.list.2 <- rbind(el.list.2,c(j,i))
					}
					
				}else if((order.m_f2i - order.m_f2j) * (order.f_m2i - order.f_m2j) >0){
					if((order.m_f2i -order.m_f2j)>0){
						el.list.2 <- rbind(el.list.2,c(i,j))
					}else{
						el.list.2 <- rbind(el.list.2,c(j,i))
					}
				}
			}
		}
	}
	return(list(swap.all = el.list,swap.ok = el.list.2))
}

test.out <- my.stable.marriage(Mm,Mf)
library(igraph)

g.swap.all <- graph.edgelist(test.out[[1]])
plot(g.swap.all)
if(length(test.out[[2]])>0){
	g.swap.ok <- graph.edgelist(test.out[[2]])
}else{
	g.swap.ok <- graph.empty(factorial(Nm))
}
plot(g.swap.ok)