入れ子立方格子

• 昨日の記事で連結した複体を作ることとその隣接行列を作ることをやった
• 複体は、単体が連結・オーバーラップしたものだった
• 今日は、立方格子が同様に連結・オーバーラップしたものとしての「立方格子の入れ子構造(複体的)」というのを考えてみる
  • 関連する話題がこちらとこちら

library(igraph)
# 軸の最大数
N <- 15
# 個々のサブ立方体の膨らみのある軸を格納する
Bs <- list()
# 個々のサブ立方体の平たい軸を格納する
Cs <- list()
# 各サブ立方体の膨らみのある軸の最大数を与える
max.n <- 3
# サブ立方体の数を指定する
k <- 10
# サブ立方体を一つずつ作っていく
for(i in 1:k){
# 第一のサブ立方体とそれ以外の処理を分ける
	if(i ==1){
# 軸集合を適当に取る
		Bs[[i]] <- sample(1:N,sample(1:max.n,1))
		Cs[[i]] <- sample(0:1,N,replace=TRUE)
		Cs[[i]][Bs[[i]]] <- -1
		#Cs[[i]] <- sample(0:1,N-length(Bs[[i]]),replace=TRUE)
	}else{
# サブ立方体の追加に当たっては、１個以上の軸で膨らむサブ立方体を追加する
		tmp.n <- sample(1:max.n,1)
# 登録済みのサブ立方体とサブサブ立方体で重ならせるので、そのサブ立方体を選ぶ
		tmp.cube <- sample(1:(i-1),1)
		a <- sample(Bs[[tmp.cube]],sample(1:min(tmp.n,length(Bs[[tmp.cube]])),1))
		print(a)
		print(tmp.n)
# それ以外は、採用の決まったa以外から取る
		b <- sample((1:N)[-a],tmp.n-length(a))
# サブ立方体の軸集合を格納する
		Bs[[i]] <- sort(c(a,b))
		Cs[[i]] <- sample(0:1,N,replace=TRUE)
		tobesame <- which(Cs[[tmp.cube]] != -1)
		Cs[[i]][tobesame] <- Cs[[tmp.cube]][tobesame]
		Cs[[i]][Bs[[i]]] <- -1

	}
}
Bs
Cs

MM <- NULL
for(i in 1:length(Bs)){
	tmp <- expand.grid(rep(list(0:1),length(Bs[[i]])))
	#tmp2[,c(Bs[[i]])] <- tmp
	flats <- which(Cs[[i]] != -1)
	tmp2 <- matrix(rep(Cs[[i]][flats],length(tmp[,1])),byrow=TRUE,nrow=length(tmp[,1]))
	tmp3 <- matrix(0,length(tmp[,1]),N)
	for(j in 1:length(flats)){
		tmp3[,flats[j]] <- tmp2[,j]
	}
	non.flats <- which(Cs[[i]] == -1)
	for(j in 1:length(non.flats)){
		tmp3[,non.flats[j]] <- tmp[,j]
	}
	
	MM <- rbind(MM,tmp3)
}

MM.check <- MM %*% 2^(1:length(MM[1,]))

dups <- duplicated(MM.check)

MM.unique <- MM[!dups,]

D <- matrix(0,length(MM.unique[,1]),length(MM.unique[,1]))
for(i in 1:(length(MM.unique[,1])-1)){
	for(j in (i+1):length(MM.unique[,1])){
		if(sum(abs(MM.unique[i,] - MM.unique[j,])) == 1){
			D[i,j] <- D[j,i] <- 1
		}
	}
}

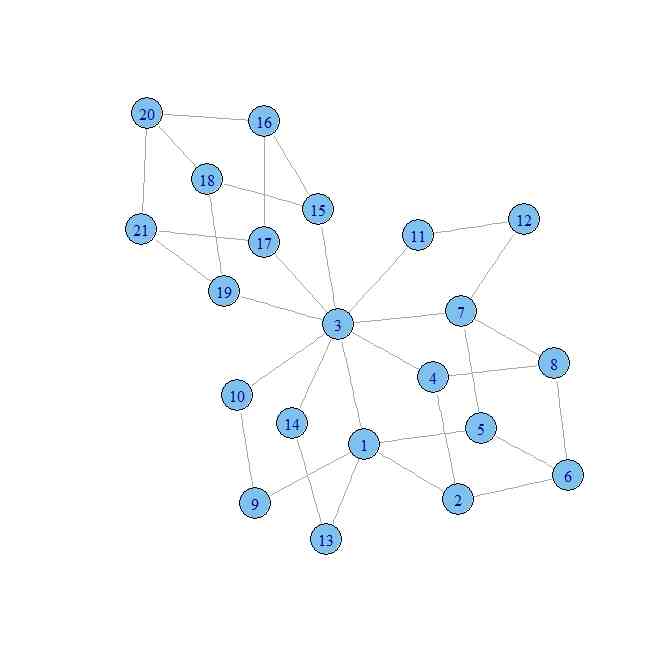
g <- graph.adjacency(D,mode="undirected")
plot(g)



sh.p <- shortest.paths(g)

sorted.path <- t(apply(sh.p,1,sort))

plot(sorted.path[,length(D[1,])])