段差が変わる階段

• こちらでサバイバルカーブを描いてみる話を聞いた
• １人、死亡が確認されるたびに、１段、下がるという階段線だと言う
• ただし、１段の段差は、そのときに「取り扱っている人数 分 の１」
• 適当に時刻データを作り、センサー情報も適当に作ると次のようになる

n <- 100
censor <- sample(0:1,n,replace=TRUE)
times <- cumsum(rexp(n))
x <- ((n-1):0)/(n:1)
v <- rep(1,length(x))
v[which(censor == 1)] <- x[which(censor ==1)]
par(mfcol = c(1,2))
plot(times,cumprod(v),type="s",ylim = c(0,1))
Data <- data.frame(Censor = censor, Time = times)
library(survival)
KMcurve <- survfit(Surv(Time, Censor)~1, data=Data)
plot(KMcurve, conf.int=FALSE, mark.time=TRUE)
par(mfcol = c(1,1))

• 全員の観測を完遂すると

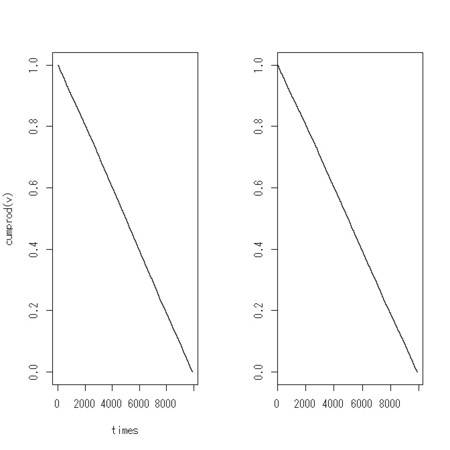
n <- 10000
# すべて、死亡まで観察する
prob <- c(0,1)
censor <- sample(0:1,n,replace=TRUE,prob=prob)
# ポツリポツリと起きること(ポアッソン過程)の事件の間隔は指数分布に従うので
# 指数乱数の累積和を生起時刻とする
times <- cumsum(rexp(n))
x <- ((n-1):0)/(n:1)
v <- rep(1,length(x))
v[which(censor == 1)] <- x[which(censor ==1)]
par(mfcol = c(1,2))
plot(times,cumprod(v),type="s",ylim = c(0,1))
Data <- data.frame(Censor = censor, Time = times)
library(survival)
KMcurve <- survfit(Surv(Time, Censor)~1, data=Data)
plot(KMcurve, conf.int=FALSE, mark.time=TRUE)
par(mfcol = c(1,1))

• ドロップアウトが生死に無関係にランダムに起きるとすると

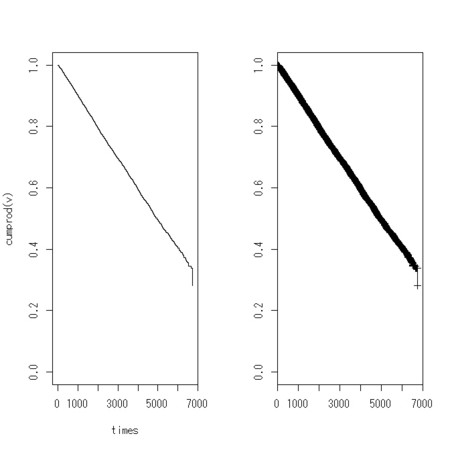
n <- 10000
perfect.pursuit <- rep(1,n)
# 死亡時刻
lambda.death <- 1
times.death <- cumsum(rexp(n,lambda.death))
# ドロップアウトはランダムに起きる
lambda.drop <- 1.5
drop.times <- sample(cumsum(rexp(n,lambda.drop)))
# ドロップアウト時刻が死亡より前なら、解析用の時刻はドロップアウトタイムで、センサーは0
# そうでないなら、解析用の時刻は死亡時刻で、センサーは1

times <- apply(cbind(times.death,drop.times),1,min)
censor <- apply(cbind(times.death,drop.times),1,order)[2,]-1

ord <- order(times)
times <- times[ord]
censor <- censor[ord]

x <- ((n-1):0)/(n:1)
v <- rep(1,length(x))
v[which(censor == 1)] <- x[which(censor ==1)]
par(mfcol = c(1,2))
plot(times,cumprod(v),type="s",ylim = c(0,1))
Data <- data.frame(Censor = censor, Time = times)
library(survival)
KMcurve <- survfit(Surv(Time, Censor)~1, data=Data)
plot(KMcurve, conf.int=FALSE, mark.time=TRUE)
par(mfcol = c(1,1))