cxxfunction()に慣れる

• 動くソースができたので、少しずつ複雑にしよう
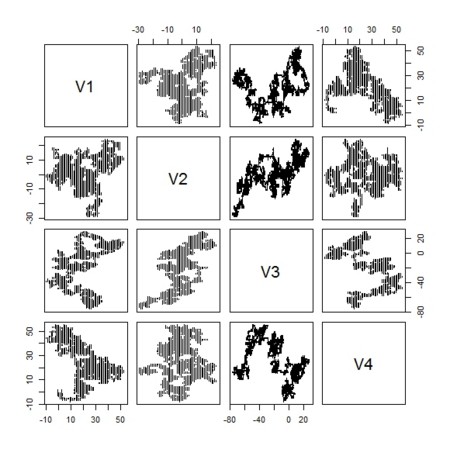
• ３次元格子から任意次元格子へ

library(Rcpp)
library(inline)
my.body2 <- '
    IntegerVector a(A);
    IntegerVector b(B);
    int c=as<int>(C);;
    int n = a.length();
    NumericMatrix x(n,c);
    for(int i=0;i<c;i++){
			x(0,i)=0;
		}
    for (int i = 1; i < n; i++) {
        for(int j = 0 ; j < c ; j++){
					x(i,j)=x(i-1,j);
				}
        x(i,a[i])+=b[i];
    }
    return wrap(x);
'

my.diff2 <- cxxfunction(sig=signature(A="integer",B="integer",C="integer"), body=my.body2, plugin="Rcpp")

T<-10000
C<-4
A<-sample(0:(C-1),T,replace=TRUE)
B<-sample(c(-1,1),T,replace=TRUE)
my.out2<-my.diff2(A,B,C)

library(rgl)
T.less<-1000
plot3d(my.out2[1:T.less,1:3],cex=0.1)

plot(as.data.frame(my.out2),cex=0.01)

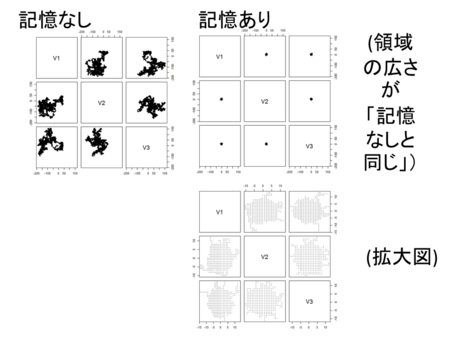
• 多次元ランダム・ウォークに制約を入れて、Self-avoiding pathにしてみる
  • Self-avoiding pathでは、どん詰まりになることがあるので、ある程度時間が経ったら「経路を忘れ」るようにする
  • 記憶が長いほど、動けないタイミングが増えたり、「びっちり」と探索したりする。記憶が短いと、どんどん動き回り、結果として、移動距離が長くなる

library(Rcpp)
library(inline)
# 記憶の長さのパラメタDを導入している
my.body3 <- '
    IntegerVector a(A);
    IntegerVector b(B);
    int c=as<int>(C);
    int n = a.length();
    int judge = 0;
    int tmpjudge = 0;
    int memoryLen=as<int>(D);
    int memorystart=0;
    NumericMatrix x(n,c);
    NumericVector tmpx(c);
    for(int i=0;i<c;i++){
			x(0,i)=0;
		}
    for (int i = 1; i < n; i++) {
        for(int j = 0 ; j < c ; j++){
					tmpx(j)=x(i-1,j);
				}
        tmpx(a(i))+=b(i);
        
        if(i<memoryLen){
					memorystart=i;
				}else{
					memorystart=memoryLen;
				}
        for(int j=i-memorystart; j<i; j++){
					tmpjudge=0;
					for(int k=0; k<c; k++){
						if(tmpx(k)==x(j,k)){
							tmpjudge+=1;
						}
					}
					if(tmpjudge==c){
						judge=1;
					}
				}
				if(judge==1){
					
				}else{
					for(int j=0;j<c;j++){
						x(i,j)=tmpx(j);
					}
				}
				judge=0;
    }
    return wrap(x);
'


my.diff3 <- cxxfunction(sig=signature(A="integer",B="integer",C="integer",D="integer"), body=my.body3, plugin="Rcpp")

T<-100000
C<-3
A<-sample(0:(C-1),T,replace=TRUE)
B<-sample(c(-1,1),T,replace=TRUE)
D<-0
my.out3.0<-my.diff3(A,B,C,D)
D<-1
my.out3.1<-my.diff3(A,B,C,D)
D<-2
my.out3.2<-my.diff3(A,B,C,D)
xlim<-ylim<-range(my.out3.0)
plot(as.data.frame(my.out3.0),cex=0.01,xlim=xlim,ylim=ylim)
plot(as.data.frame(my.out3.1),cex=0.01,xlim=xlim,ylim=ylim)
plot(as.data.frame(my.out3.2),cex=0.01,xlim=xlim,ylim=ylim)

• こちらへ続く(情報を整理編)