ぐるぐる回るために - ryamadaのコンピュータ・数学メモ

円(周)は２次元空間におかれたぐるり
球(面)は３次元空間におかれたぐるり
n階の常微分方程式で、どこが初期値でも発散しないようにする一つのやりかたをこちらに書いた
導関数の値 $(y^0,y^1,...,y^{n-1})$ を位置座標として、その位置ベクトルを半径とするn次元球面の接面を運動ベクトルとして定めた
$(y^1,y^2,...,y^{n-1},f$ がその運動ベクトルで、第１から第n-1成分までは座標によって決まっており、この運動ベクトルが接面上にあるためには $f$ の値を適当に定めるしかなく、運動ベクトルは一意に決まる
このようなベクトルがどのようなものであるかをn=3の場合について示した
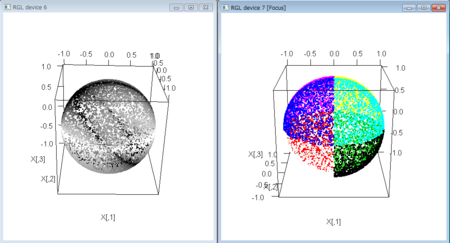
- (1)ベクトルの長さ(速さの絶対値)(モノクロ図)
  - 速さは、第３軸の値(y2=0)が0のときに無限大(白)に、それと９０度の角度で交わる面(y1=0)と４５度で交わる線(y0+y2=0)が速さ０(黒)となっている
- (2)ベクトルの向きを「象限」で分割(カラー図)
  - 進むべき方向が位置ベクトルによってうまくぐるりとなるようになっていることが色彩的にわかる

ここでは、原点を中心としたn次元球で作ったが、適当な形を与えた「アトラクタ」を中心にすれば、形は変えられる

Npt<-10000
n<-3
X<-matrix(rnorm(Npt*n),Npt,n)

X<-X/sqrt(apply(X^2,1,sum))
#apply(X^2,1,sum)

Y<-rep(0,Npt)

for(i in 1:(n-1)){
	Y<-Y+X[,i]*X[,i+1]
}


Y<-(-Y/X[,n])
Y<-log(abs(Y))
qtl<-quantile(Y,c(0.05,0.95))
Y[which(Y<qtl[1])]<-qtl[1]
Y[which(Y>qtl[2])]<-qtl[2]

col=gray((Y-qtl[1])/(qtl[2]-qtl[1]))
library(rgl)
plot3d(X,col=col)
#plot3d(X,col=gray(order(Y)/Npt))

sX<-sign(X)
sX<-(sX-(-1))/2
open3d()
col2<-sX[,1]*1+sX[,2]*2+sX[,3]*4
plot3d(X,col=col2)

for()ループを使わないためにはこちらを