- 最小全域木の多次元化についてこちらにメモした
- 多次元化する別の方法について考えてみる
- 最小全域木をもう一度見直す
- 最小全域木作成のアルゴリズムを確認する
- すべての点が「辺」でつながるように持っていく
- 「辺」は1次元的なもの
- (作りうる)すべての「辺」のうち「もっとも小さな」「辺」を採用する
- 辺によってつながっている「塊」とつながっている「辺」で、「塊」にまだつながっていない「点」とつながっているもののうち、「もっとも小さな」「辺」を「塊」につなげる
- すべての点が「塊」に属するまで続ける
- このアルゴリズムで、「辺」の1次元的な部分を「高次元的」に変えることとする
- すべての点が「高次元的辺」でつながるように持っていく
- 「高(k)次元的辺」は「k次元的」なもの
- (作りうる)すべての「高次元的辺」のうち「もっとも小さな」「子次元的辺」を採用する
- 高次元的辺によってつながっている「塊」とつながっている「高次元的辺」で、「塊」にまだつながっていない「点」とつながっているもののうち、「もっとも小さな」「高次元的辺」を「塊」につなげる
- すべての点が「塊」に属するまで続ける
- 「高(k)次元的辺」はk+1個の点が定める何か(k=1のときは、k+1=2点が定める「辺」)
- 「高(k)次元的辺」の大小を定めたい。k=1のときには、辺の長さを用いた(ユークリッド最小全域木の場合)
- 一番自然には、「(高次元)体積」だろう
- このようにして、1,2,...次最小全域木が定義できて、その「高次元的辺」の値の和も定義できる
- いくつか考えることがある
- [tex:i
- 含まれることが確実ならば、低次の最小全域木を得てから、一段階、高次の最小全域木を探しに行くのが効率的なように思われる
- 含まれるなら、i次最小全域木の「値」とi+1次最小全域木の値との比は、「i+1次な『高さ』」となって、その高さが低いことは、低次的にまとまりがよいことを意味するのではないかと思われる
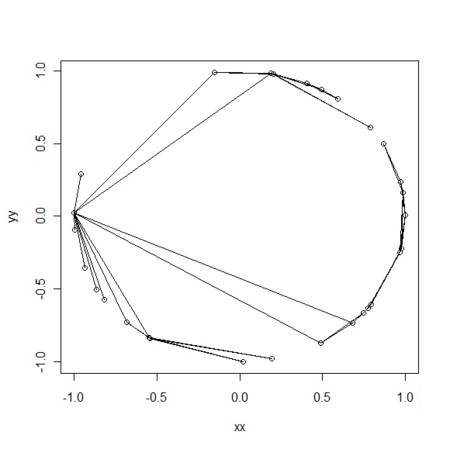
- 低次最小全域木から高次化しない場合(2次元空間の点に2次元最小全域木をいきなり取る)を下に示す。できた「2次元全域木」はちょっとイメージが違う(定義次第だが)。
- ボロノイ図との関係はどうなるのか、も気になる
SimplexVolume<-function(x,Factorial=FALSE){
n<-length(x[,1])
d<-apply(x,2,FUN="diff")
if(Factorial){
ret<-log(abs(det(d))) - lfactorial(n-1)
}else{
ret<-log(abs(det(d)))
}
return(ret)
}
SimplexVolume2<-function(x,Factorial=FALSE){
n<-length(x[,1])
tmpX<-t(x[2:n,])-x[1,]
if(n==2){
ret<-log(sqrt(sum(tmpX^2)))
}else{
svd.out<-svd(t(tmpX))
tmpX<-t(tmpX)%*%svd.out[[3]]
ret<-SimplexVolume(rbind(rep(0,length(tmpX[1,])),tmpX),Factorial=Factorial)
}
return(ret)
}
k<-3
df<-5
Npt<-5
X<-matrix(runif(Npt*df),ncol=df)
X<-diag(rep(1,Npt))
library(gtools)
cmb<-combinations(Npt,k)
cmb
Ncmb<-length(cmb[,1])
w<-rep(0,Ncmb)
for(i in 1:Ncmb){
tmpX<-X[cmb[i,],]
tmpn<-length(tmpX[,1])
tmpX<-t(tmpX[2:tmpn,])-tmpX[1,]
if(tmpn==2){
w[i]<-log(sqrt(sum(tmpX^2)))
}else{
svd.out<-svd(t(tmpX))
print(svd.out)
print(tmpX)
print(svd.out[[3]])
tmpX<-t(tmpX)%*%svd.out[[3]]
print(tmpX)
w[i]<-SimplexVolume(rbind(rep(0,length(tmpX[1,])),tmpX),Factorial=TRUE)
}
}
exp(w)
k<-3
df<-2
Npt<-30
X<-matrix(runif(Npt*df),ncol=df)
t<-runif(Npt)*2*pi
xx<-cos(t)
yy<-sin(t)
X<-cbind(xx,yy)
library(gtools)
cmb<-combinations(Npt,k)
Ncmb<-length(cmb[,1])
w<-rep(0,Ncmb)
for(i in 1:Ncmb){
tmpX<-X[cmb[i,],]
w[i]<-SimplexVolume2(tmpX,Factorial=TRUE)
}
exp(w)
cmb2<-cmb
print(cmb2)
selected<-rep(0,Npt)
h<-cmb[which(w==min(w)),]
selected[h]<-1
ss<-which(selected==1)
for(i in 1:length(ss)){
cmb2[which(cmb2==ss[i])]<-0
cmb2<-t(apply(cmb2,1,sort))
}
while(sum(selected)<Npt){
candidates<-which((cmb2[,k-1]==0) & (cmb2[,k]!=0))
wc<-w[candidates]
minw<-candidates[which(wc==min(wc))]
h<-rbind(h,cmb[minw,])
selected[cmb[minw,]]<-1
newselect<-cmb2[minw,k]
cmb2[which(cmb2==newselect)]<-0
cmb2<-t(apply(cmb2,1,sort))
print(cmb2)
}
print(h)
plot(X)
for(i in 1:length(h[,1])){
for(j in 1:(length(h[i,]))){
for(j2 in (j):length(h[i,])){
segments(X[h[i,j],1],X[h[i,j],2],X[h[i,j2],1],X[h[i,j2],2])
}
}
}
dM<-dist(X)
library(vegan)
stree<-spantree(dM)
stree
