ryamadaのコンピュータ・数学メモ

2011-07-09

円に関する反転

原点を中心とする半径１の円について円の内側の図形を外側に反転させるとき
原点Oからの距離が $0 < r\le 1$ の点Pは、OPの延長線上であって、距離 $\frac{1}{r}$ の点P'に移される
また、PとP'とを通る円は、原点からの距離が $\frac{r^2+1}{2r}$ でありPP'に垂直な直線上に中心を持ち、このような円の弧と、反転の基準である円(今は単位円)の弧とは、直交する
この円に直交する円はこの反転によって、自身に移される

Npt<-5

ts<-runif(Npt)*pi/2
rs<-runif(Npt)*0.8+0.1

xs<-rs*cos(ts)
ys<-rs*sin(ts)
xs2<-1/rs*cos(ts)
ys2<-1/rs*sin(ts)

xlim<-ylim<-range(c(xs2,ys2,xc,yc))
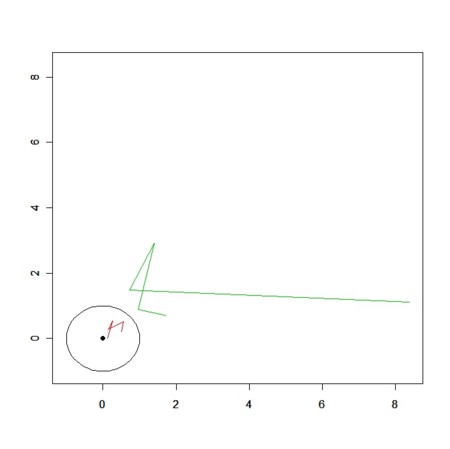
plot(xc,yc,xlim=xlim,ylim=ylim,type="l",main="",xlab="",ylab="")

par(new=TRUE)

plot(rs*cos(ts),rs*sin(ts),,xlim=xlim,ylim=ylim,type="l",main="",xlab="",ylab="",col=2)

par(new=TRUE)
plot(1/rs*cos(ts),1/rs*sin(ts),,xlim=xlim,ylim=ylim,type="l",main="",xlab="",ylab="",col=3)

points(0,0,pch=19)