n <- 1000
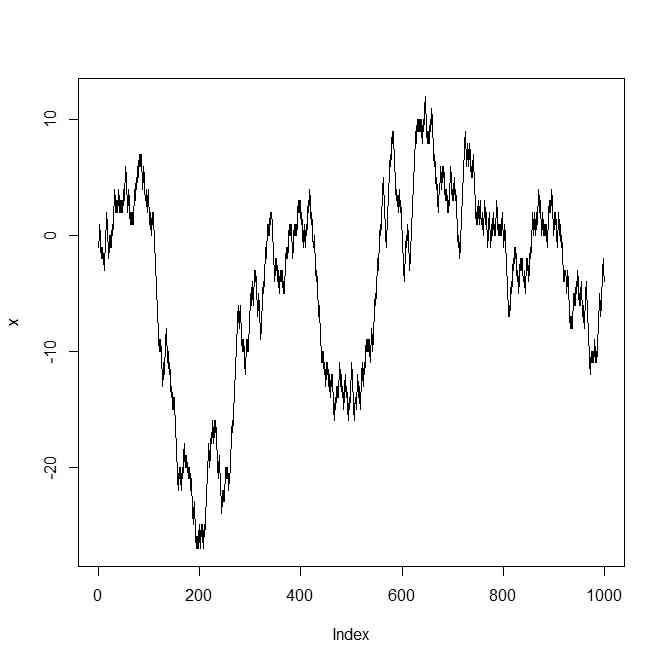
x <- cumsum(sample(c(-1,1),replace=TRUE,n))
plot(x,type="l")
-
- すべての時刻で、位置の期待値は0で、分散は時刻tに対して、t

n <- 1000
n.trial <- 10000
X <- matrix(sample(c(-1,1),replace=TRUE,n*n.trial),ncol=n.trial)
X. <- apply(X,2,cumsum)
par(mfrow=c(2,2))
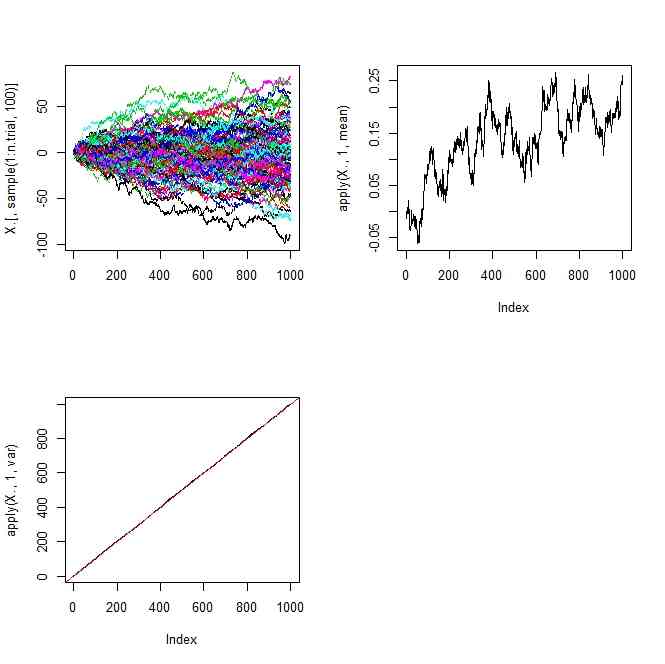
matplot(X.[,sample(1:n.trial,100)],type="l")
plot(apply(X.,1,mean),type="l")
plot(apply(X.,1,var),type="l")
abline(0,1,col=2)
par(mfcol=c(1,1))
- 少し拡張して、一歩を正規分布にするとウィーナー過程
- 見かけは、ほとんど変わっていない(一歩の平均を0にしてあるから。平均を0でなくしてもよい)
- 時刻tでの位置の期待値と分散も同様に0とt
n <- 1000
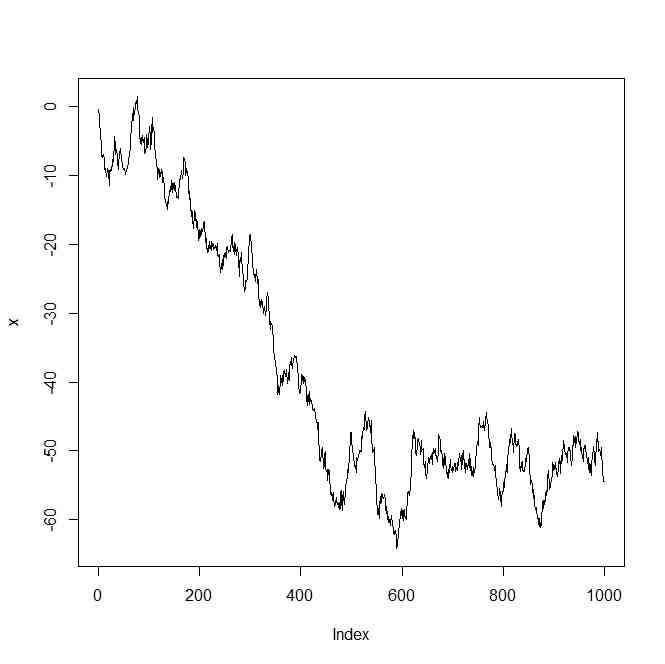
x <- cumsum(rnorm(n))
plot(x,type="l")
n <- 1000
n.trial <- 10000
X <- matrix(rnorm(n*n.trial),ncol=n.trial)
X. <- apply(X,2,cumsum)
par(mfrow=c(2,2))
matplot(X.[,sample(1:n.trial,100)],type="l")
plot(apply(X.,1,mean),type="l")
plot(apply(X.,1,var),type="l")
abline(0,1,col=2)
par(mfcol=c(1,1))
- これを別の視点から見てやる(Fractional brownian motion (日本語訳は非整数ブラウン運動))
- 上では一歩の大きさと向きを確率変数にしていた
- 今度は、自己相似過程であって、ガウス過程であって、連続であって、0からスタートして、増分の期待値が0であって、増分の分散が、2つの時刻の差の絶対値の定数倍である、と言う、定義を先にする。それは結局、ウィーナー過程で、一歩の平均が0で分散をいくつかに固定したものになる
- 何も面白くなさそうだけれど、ちょっと違う
- 増分の分散を2つの時刻の差の絶対値の定数倍の代わりに、差の絶対値の定数乗の定数倍とし、ウィーナー過程を、「定数乗」のところがたまたま1乗である場合とみなす
- こうすることで、ウィーナー過程に似ているけれど、軌道の滑らかさ・ガタボコ加減に違いを入れることができるようになる
- この「定数乗」のところを、ハーストパラメタ(H)を使って表し、0 < H < 1として、ウィーナー過程をH=0.5のときに対応付けることになっている
- Fractional brownian motionのシミュレーションをしてみよう
- いつも、次にどんな一歩をとるかは同じなのに、結果として滑らかになったりガタボコになったりするわけで、正規乱数の積み重ねではだめだ(それではウィーナー過程になってしまう)
- その方法として、midpoint法というのがある(この方法を別法と比べているので、アルゴリズムに関する説明がある文書は、こちら、アルゴリズムはこちら)
- 簡単に言うと、ある2時刻間で、どのくらい違う点になるか、は分散がわかれば、乱数指定できるので、それを先に決め、その上で、その途中経過の中点の位置を、両端の点との時間差と分散に合わせて決める、というプロセスを繰り返してだんだん細かくしていく、という方法
- ウィーナー過程をこれでシミュレーションするのは、重くなるだけだけれど、ちゃんとうまくいくことを確認
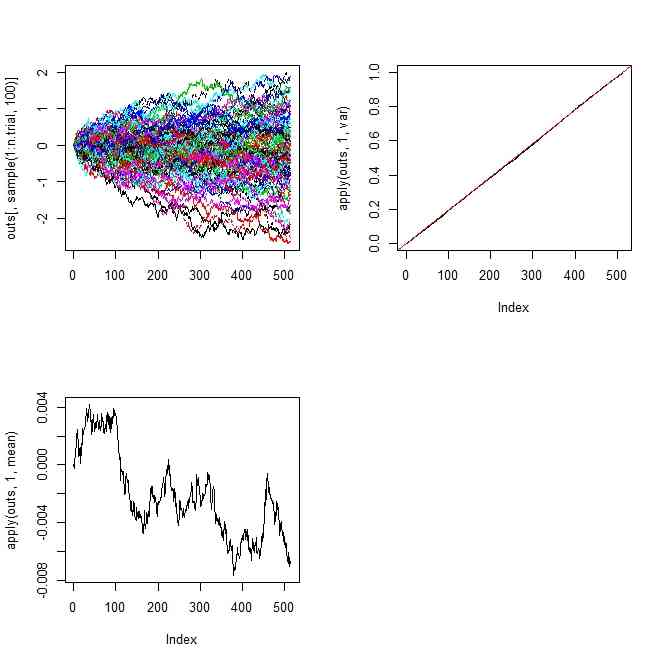
- どこがうまくいっているかっていえば、時刻ごとの分散が予想通りだということ
my.midpoint <- function(H=0.5,m=0,t=1,n.step){
X <- list()
X0 <- c(0,0)
X1 <- rnorm(1,m,t^(H*2))
X[[1]] <- rbind(X0,X1)
for(i in 2:n.step){
n.pre <- length(X[[i-1]][,1])
tmpx <- tmpy <- rep(0,n.pre*2-1)
tmpx[1] <- X[[i-1]][1,1]
tmpy[1] <- X[[i-1]][1,2]
cnt <- 2
for(j in 1:(n.pre-1)){
tmpX <- 1/2*(X[[i-1]][j,1] + X[[i-1]][j+1,1])
tmpY <- 1/2*(X[[i-1]][j,2] + X[[i-1]][j+1,2]) + sqrt((1-2^(2*H-2))/(2^(2*(i-1)*H)))*rnorm(1)
tmpx[c(cnt,cnt+1)] <- c(tmpX,X[[i-1]][j+1,1])
tmpy[c(cnt,cnt+1)] <- c(tmpY,X[[i-1]][j+1,2])
cnt <- cnt+2
}
X[[i]] <- cbind(tmpx,tmpy)
}
X
}
H <- 0.5
n.step <- 10
out <- my.midpoint(H=H,n.step=n.step)
plot(out[[n.step]],type="l")
n.trial <- 10000
outs <- matrix(0,2^(n.step-1)+1,n.trial)
for(i in 1:n.trial){
tmp <- my.midpoint(H=H,n.step=n.step)
outs[,i] <- tmp[[n.step]][,2]
}
par(mfcol=c(2,2))
matplot(outs[,sample(1:n.trial,100)],type="l")
plot(apply(outs,1,mean),type="l")
plot(apply(outs,1,var),type="l")
abline(0,1/(2^(n.step-1)+1),col=2)
par(mfcol=c(1,1))
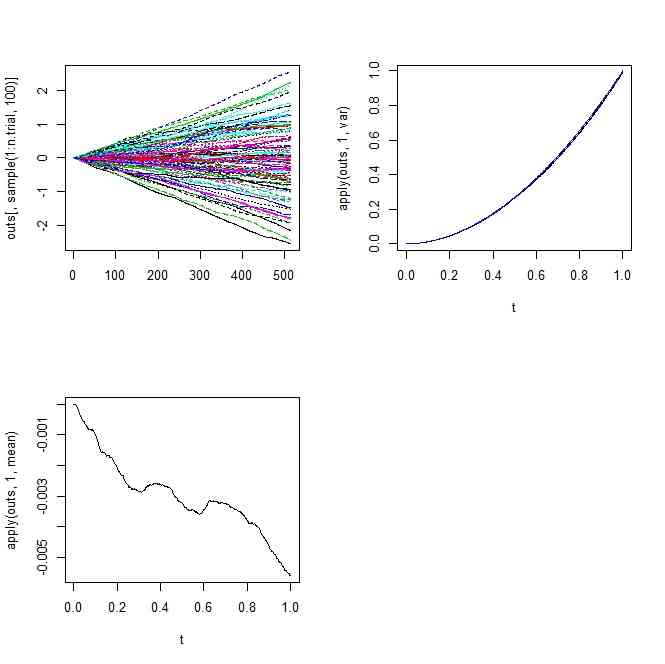
- じゃあ、Fractional brownian motionでウィーナーではない場合をやってみる
H <- 0.95
n.step <- 10
n.trial <- 10000
outs <- matrix(0,2^(n.step-1)+1,n.trial)
for(i in 1:n.trial){
tmp <- my.midpoint(H=H,n.step=n.step)
outs[,i] <- tmp[[n.step]][,2]
}
par(mfcol=c(2,2))
matplot(outs[,sample(1:n.trial,100)],type="l")
t <- seq(from=0,to=1,length=2^(n.step-1)+1)
v <- t^(2*H)
plot(t,apply(outs,1,mean),type="l")
plot(t,apply(outs,1,var),type="l")
points(t,v,col=4,type="l")
par(mfcol=c(1,1))
-
- ガタボコの場合
- 分散の理論カーブに対して、シミュレーションの場合に、ずれがある。0,1,0.5など「早めにシミュレーションした時点」の分散はうまくいっているが、シミュレーションが後になればなるほど、理論値よりもずれが大きい、というパターン
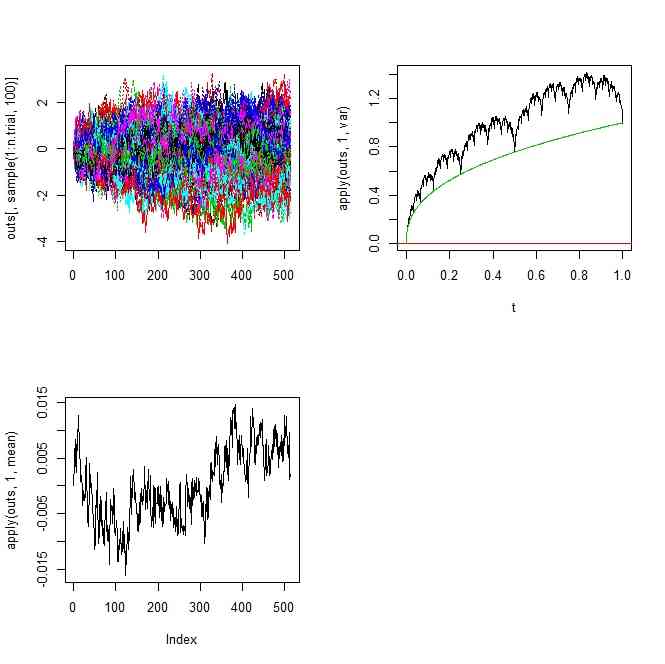
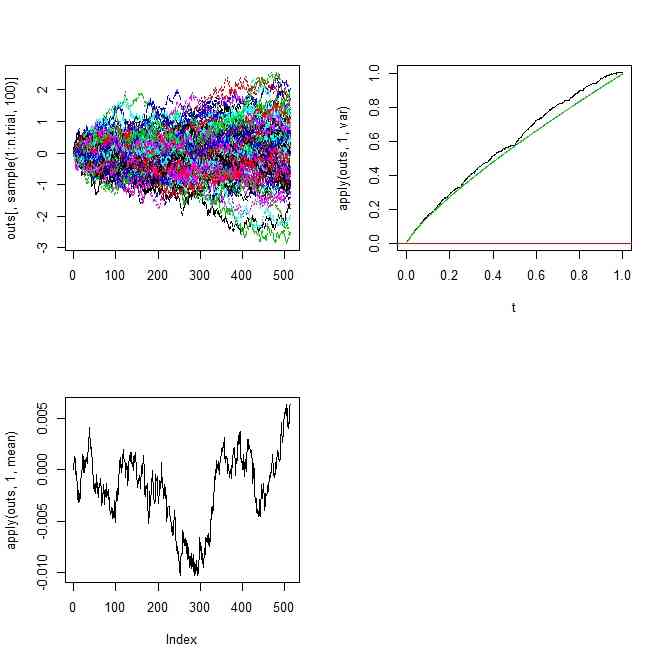
- H=0.2
-
- これは、ガタボコな場合、分割を繰り返しても、新たな点の座標を決めるときに用いる正規乱数の分散が結構大きいままであること、また、分割が後になるほど、「その前に決めた値」が「あるべき値」よりも分散が大きめに出ている、ことをひきずっているので、ばらつきを累積してしまうことが関係しているだろう(その累積も見越して、ある分割のときのばらつきを少し小さ目にする、とか言う工夫はないのか…とは思うのだが)
H <- 0.2
n.step <- 10
n.trial <- 10000
outs <- matrix(0,2^(n.step-1)+1,n.trial)
for(i in 1:n.trial){
tmp <- my.midpoint(H=H,n.step=n.step)
outs[,i] <- tmp[[n.step]][,2]
}
par(mfcol=c(2,2))
matplot(outs[,sample(1:n.trial,100)],type="l")
t <- seq(from=0,to=1,length=2^(n.step-1)+1)
v <- t^(2*H)
plot(t,apply(outs,1,mean),type="l")
plot(t,apply(outs,1,var),type="l")
points(t,v,col=4,type="l")
par(mfcol=c(1,1))
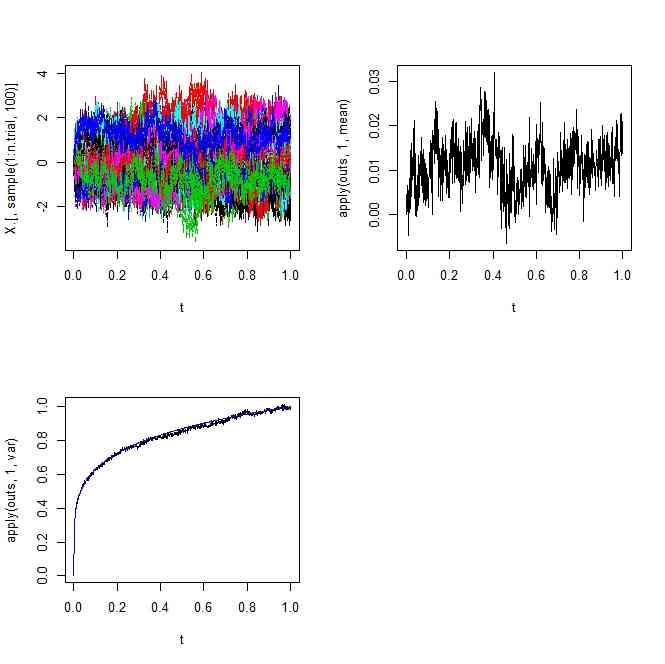
- さて、このFractional brownian motionだが、増分の平均、増分の分散をパラメタ表示できたのだが、もう一歩進めて、共分散を見てみる
- この共分散行列を使ってシミュレーションしてみる
- 共分散行列があれば、多変量正規乱数を発生させればよい
-
- すべての時点を「平等に」計算しているから、ばらつきの持越しが発生していない
- ちなみに、この行列は、時刻が0に近ければ値のばらつきは小さく、時刻が後になるほどばらつくことと、二時刻間の値の違いのばらつきが二時刻の違いが大きいほど
library(mvtnorm)
H <- 0.1
t <- seq(from=0,to=1,length=1000)
d <- as.matrix(dist(t))
t2 <- t^(2*H)
D <- 1/2*(outer(t2,t2,"+") - d^(2*H))
n.trial <- 10000
outs <- t(rmvnorm(n.trial,sigma=D))
v <- t^(2*H)
par(mfrow=c(2,2))
matplot(t,X.[,sample(1:n.trial,100)],type="l")
plot(t,apply(outs,1,mean),type="l")
plot(t,apply(outs,1,var),type="l")
points(t,v,col=4,type="l")
par(mfcol=c(1,1))
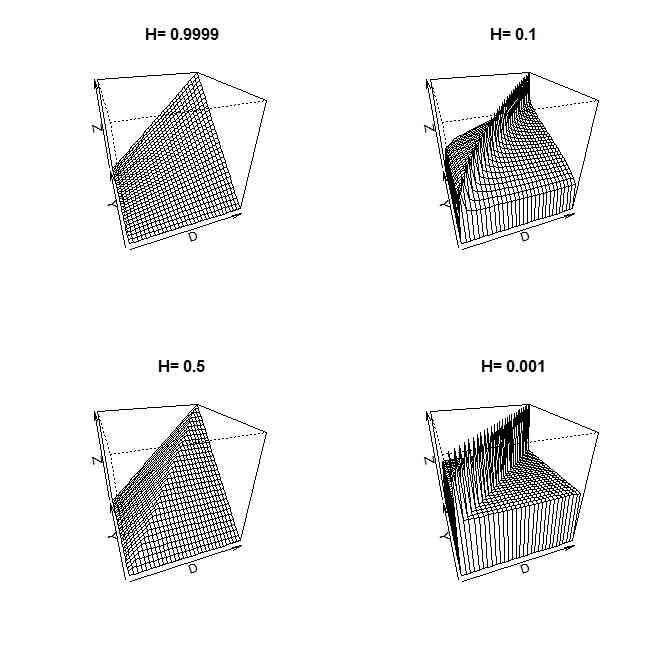
- このうまいこと行く共分散行列がどんなものかを図にしてみる
- わかりやすいのはHが小さいときだろうか。対角線に分散共分散の大きい値があって、それ以外は小さい。要するに、自身とは関係があるが、自身以外との関連はない、という場合
- Hを大きくすると滑らかな軌道になるが、始点と終点とは、その距離に応じてある分散を持つから、始点と終点の値は近いわけがなく、関連がないはず。さらに言えば、始点から有限な距離があるときはその2点の間には関連がないので、共分散行列の値も0。ただし、その原則は有りながら、距離が近い者同士では値が近くなる。結果として、始点と他のすべての点との間に関連はないが、対角線では値が大きくなる。その両方の傾向を満足するために、(0,0)で0、x=0,y=0で0、(1,1)で1、を満足しつつ、2点間の距離が同じであれば、始点から遠いほど大きな値をとる、ということになる
- ちなみにウィーナー過程では、その原則を守りつつ、凸多面体のようになっている
par(mfcol=c(2,2))
H <- 0.9999
t <- seq(from=0,to=1,length=30)
d <- as.matrix(dist(t))
t2 <- t^(2*H)
D <- 1/2*(outer(t2,t2,"+") - d^(2*H))
persp(D,theta=-20,phi=30,main=paste("H=",H))
H <- 0.5
t <- seq(from=0,to=1,length=30)
d <- as.matrix(dist(t))
t2 <- t^(2*H)
D <- 1/2*(outer(t2,t2,"+") - d^(2*H))
persp(D,theta=-20,phi=30,main=paste("H=",H))
H <- 0.1
t <- seq(from=0,to=1,length=30)
d <- as.matrix(dist(t))
t2 <- t^(2*H)
D <- 1/2*(outer(t2,t2,"+") - d^(2*H))
persp(D,theta=-20,phi=30,main=paste("H=",H))
H <- 0.001
t <- seq(from=0,to=1,length=30)
d <- as.matrix(dist(t))
t2 <- t^(2*H)
D <- 1/2*(outer(t2,t2,"+") - d^(2*H))
persp(D,theta=-20,phi=30,main=paste("H=",H))
- と、このように何をしているのかがだいたいわかったら、RのパッケージRandomFieldsに戻ろう→こちら
= 0]









