2014-09-11

曲線、２Ｄ

微分幾何曲線曲率

Cartan for Beginnnersをぱらぱらめくって(昨日の記事)、まずは２Ｄ平面上の曲線を評価しよう
観察点は離散的
十分滑らかとしよう(実観測は、平滑化すれば、『元の正しい曲線』になっているものとしておく)
観察点には座標がある
隣接する観察点の中間点に、接ベクトルの推定されたものがあるとする
接ベクトルが推定された点が並んでいるが、その隣接する２点の中間点に、接ベクトルの変化が推定される
今２Ｄなので、この「接ベクトル」の変化を表すウェッジ積はスカラーになる(３Ｄなら垂直方向のベクトルになるところだが)
そのウェッジ積を２点間の距離(これは、観測点を結んだ折れ線をたどった長さで代用する)を進む間に起きた変化であるとして、「単位弧長あたりの変化」とすれば、これは符号付きの曲率
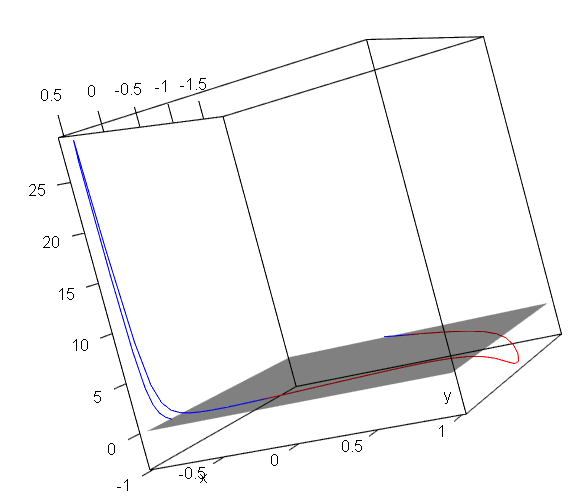
曲線を観察したら、それに沿って「符号付き曲率」も観察されているので、「曲線のための２次元」と「符号付き曲率のための１次元」の｢併せて３次元」の情報があるものとしてプロットしてみると、「符号付き曲率情報込み」の曲線が３次元プロットできる
このようにして得られる「符号付き曲率情報込みの曲線」が二つあったら、その異同は、２曲線上の点に１対１対応があれば、その対応点間の３次元空間での「距離」の積分は「２曲線の距離(曲率情報加味)」となるのではなかろうか
そのような「曲線間の距離」は「曲率情報を加味」せずに２Ｄ曲線として計算することもできるが、「込み」と「非込み」とでは値が変わり、多数の曲線の相互距離の大小関係は「込み」と「非込み」とで変わるから、「込み」で評価すれば、「符号付き曲率」を盛り込みたいという気持ちが入った尺度になっているのではないか、とそんな感じ

# 二次元曲線の処理

my.2D.curve <- function(X){
	n.pt <- length(X[,1]) # 観測点の数
	Xpre <- X[-n.pt,]
	Xpost <- X[-1,]
	X.loc <- (Xpre+Xpost)/2 # 接線方向ベクトルが観察された「座標」
	X.locpre <- X.loc[-(n.pt-1),]
	X.locpost <- X.loc[-1,]
	X..loc <- (X.locpre+X.locpost)/2 # 接線方向ベクトルの変化、が観察された「座標」
	
	X. <- apply(X,2,diff)
	L <- sqrt(apply(X.^2,1,sum))
	X.st <- X./L # 接線方向の単位ベクトル
	
	X.stpre <- X.st[-(n.pt-1),]
	X.stpost <- X.st[-1,]
	Lpre <- L[-(n.pt-1)]
	Lpost <- L[-1]
	Lmean <- (Lpre+Lpost)/2
	crv <- (X.stpost[,1] * X.stpre[,2] - X.stpost[,2] * X.stpre[,1])/Lmean
	return(list(X=X,X.loc=X.loc,X..loc=X..loc,X.=X.,X.st=X.st,crv=crv,L=L))
}

t <- seq(from=0,to=1,length=50)*0.9
ut <- exp(t) # 素直でない媒介変数にしておく
#ut <- t
x <- exp(t)*cos(ut)
y <- sin(ut*4)
X <- cbind(x,y)
crv.out <- my.2D.curve(X)

plot(crv.out$X,asp=TRUE)
points(crv.out$X..loc,pch=20,cex=abs(crv.out$crv)/min(abs(crv.out$crv))*0.1,col=sign(crv.out$crv)+3)


plot(X,pch=20,cex=abs(crv.out$crv)/min(abs(crv.out$crv))*0.001,col=sign(crv.out$crv)+3,asp=TRUE)
plot(X)

library(rgl)
plot3d(cbind(crv.out$X..loc,crv.out$crv),type="l",col=sign(crv.out$crv)+3)
planes3d(0,0,1,0, alpha=0.5)