 の解を考える
の解を考える と固有値分解し、3個の固有値k1,k2,k3がすべて実数であるとしk1 > k2 > k3とする
と固有値分解し、3個の固有値k1,k2,k3がすべて実数であるとしk1 > k2 > k3とする なので
なので とすれば
とすれば
- 結局、

- これをz=1平面を射影平面P2としたときに、どのような曲線が描かれるか、という話
- P2上の座標はA...Iと書き換えて
 と書ける
と書ける
- 今、「形」を問題にしているので、適当な平行移動と回転と拡縮をしても一般性を失わないから、この曲線がP2上の3点(1,0),(-1,0),(u,v);v>0を頂点とする3角形内の曲線になるようにすることができる
- ここで、3頂点座標は、Vの列ベクトルを同次座標と見たときのP2上の点になる(Mの固有ベクトルに対応する点のこと)
- また、この曲線は3頂点のうちの2頂点に収束するカーブになる。3頂点のうち、どの2点が収束する2頂点となるかは、最大のk1と最小のk2とに対応する固有ベクトルに対応する2頂点である(tを無限小、無限大にしたときのP2上の座標がどうなるかを考えればよい)
- したがって、G=A,D=0,C=-I,F=0,B=uH,E=vHとなる
- さて、今ここでは、射影平面が現実世界であるとして、そこにあるカーブがあって、そこから、A-I,k1,k2,k3を推測したいとする
- P2上の曲線が、(ru,rv);0

- 分母分子を
 で割れば
で割れば

- 今、拡縮とかは気にしないし、「曲線」の形を考えているから、パラメタtも勝手にシフト・伸縮してよいので、t=0のときに(ru,rv)を通るようにすることができて、
 なので、
なので、
- ここまででわかったことは
 なる行列がk1,k2,k3の値によらず、
なる行列がk1,k2,k3の値によらず、 と
と と
と の3頂点で規定され、(1,0)と(-1,0)とに収束し、かつ、(ru,rv)なる点を通る曲線である、ということ
の3頂点で規定され、(1,0)と(-1,0)とに収束し、かつ、(ru,rv)なる点を通る曲線である、ということ
- 実際、A',
 の値がrで規定されているのは、初期値X0,Y0,Z0を適当に取ったことによる影響であって、もとの連立微分方程式のMでは、固有ベクトルのP2像を規定することだけに意味がある。以下のように、(ru,rv)がt=0のときに通るようにすれば、Mの値はかなり自由
の値がrで規定されているのは、初期値X0,Y0,Z0を適当に取ったことによる影響であって、もとの連立微分方程式のMでは、固有ベクトルのP2像を規定することだけに意味がある。以下のように、(ru,rv)がt=0のときに通るようにすれば、Mの値はかなり自由
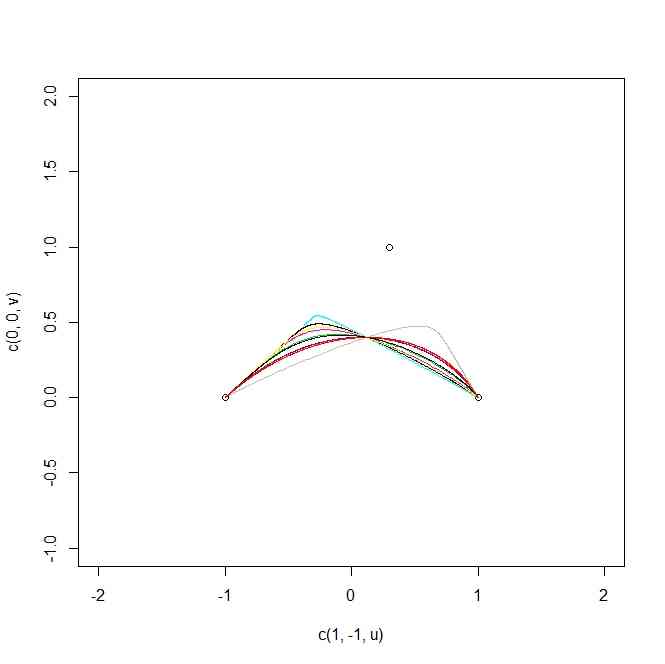
- 3つの固有値の取り方で曲線の形が変わるから、もう1点、通過点を与えれば、k1,k2,k3に制約が入って曲線の形は確定する
u <- 0.3
v <- 1
r <- 0.4
n.iter <- 1000
ret <- list()
t <- seq(from=-10,to=10,length=1000)
for(ii in 1:n.iter){
A <- rnorm(1)*10
C <- rnorm(1)*10
M <- matrix(c(A,0,A,u,v,1,C,0,-C),3,3)
lambdas <- sort(rnorm(3))
x.init <- c(r*u,r*v,1)
x.init.2 <- solve(M) %*% x.init
X <- matrix(0,length(t),3)
for(i in 1:3){
X[,i] <- x.init.2[i]*exp(t*lambdas[i])
}
Y <- t(M %*% t(X))
ret[[ii]] <- cbind(Y[,1]/Y[,3],Y[,2]/Y[,3])
}
plot(c(1,-1,u),c(0,0,v),xlim=c(-2,2),ylim=c(-1,v+1))
for(ii in 1:length(ks)){
points(ret[[ii]],type="l",col=ii)
}
の解を考える
と固有値分解し、3個の固有値k1,k2,k3がすべて実数であるとしk1 > k2 > k3とする
なので
とすれば
と書ける
と
と
の3点
で割れば
なので、
なる行列がk1,k2,k3の値によらず、
と
と
の3頂点で規定され、(1,0)と(-1,0)とに収束し、かつ、(ru,rv)なる点を通る曲線である、ということ
の値がrで規定されているのは、初期値X0,Y0,Z0を適当に取ったことによる影響であって、もとの連立微分方程式のMでは、固有ベクトルのP2像を規定することだけに意味がある。以下のように、(ru,rv)がt=0のときに通るようにすれば、Mの値はかなり自由
