複比でできた三角形上の直線

• 連立常微分方程式と射影幾何、複比の関係はこちら。固有値の差をパラメタとした指数関数の和が複比を定めることがわかっている(こちら)
  • この複比を標準化すればのような関数が表れる
• 今、三角形があって、その２辺に、辺の両端を収束点とする複比数列があるとする
• これは、射影前の３次元空間において、固有ベクトルに関して両対数グラフ的に作った格子点の軸上の刻みの点に相当する
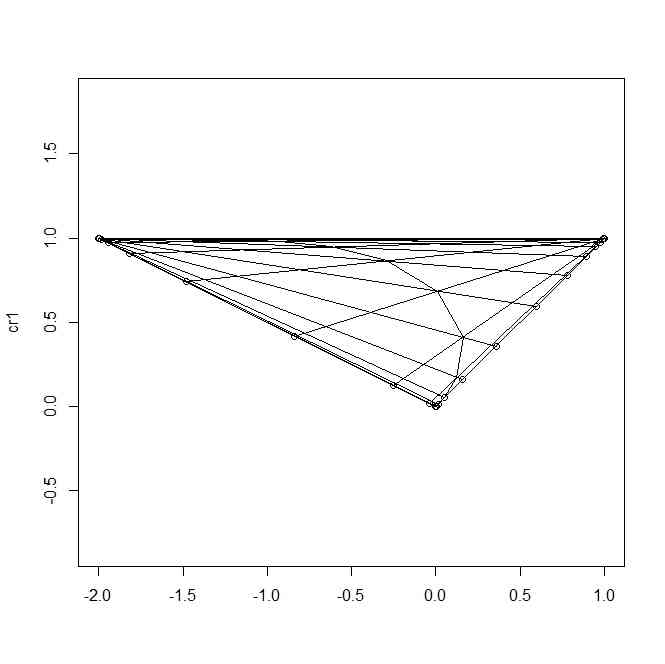
• これを射影した２次元平面上の三角形に「両対数グラフだったときに方形格子」になっていたはずのものがどのように現れるのかを描く
• さらに、「両対数グラフだったときの方形格子に関して個々の格子の対角線を通る『直線』」が射影後にどのようになるかを、射影した格子の格子点を結ぶことで表してみる

# S字曲線を作成する関数
hill1 <- function (dose, parm){
	parmMat <- matrix(c(parm, 1), 1, 5, byrow = TRUE)
	parmMat[, 2] + (parmMat[, 3] - parmMat[, 2])/((1 + exp(parmMat[, 1] * (dose - parmMat[, 4])))^parmMat[, 5])
}

a <- 2
b <- 3
k <- 4
t <- seq(from=-5,to=5,length=100)

y <- a + b * exp(k*t) / (exp(k*t)+exp(-k*t))

plot(t,y)

my.cr <- function(n,k,N=10){
	t <- seq(from=-N,to=N,length = n)
	(exp(k*t)/(exp(k*t)+exp(-k*t)))^2
}

a <- 1
b <- -2

n <- 100
ka <- 2
kb <- 3
cr1 <- my.cr(n,ka)
cr2 <- my.cr(n,kb)

Xa <- cbind(a*cr1,cr1)
Xb <- cbind(b*cr2,cr2)

plot(rbind(Xa,Xb),asp=TRUE)
for(i in 1:n){
	segments(b,1,Xa[i,1],Xa[i,2])
	segments(a,1,Xb[i,1],Xb[i,2])
}

s <- sample(1:n,2,replace=TRUE)
s <- c(1,2)
min.s <- min(s)
max.s <- max(s)

my.cross.2.seg <- function(v1,v2,v3,v4){
	t <- ((v2[1]-v4[1])/(v1[1]-v2[1]) - (v2[2]-v4[2])/(v1[2]-v2[2]))/((v3[1]-v4[1])/(v1[1]-v2[1]) - (v3[2]-v4[2])/(v1[2]-v2[2]))
	t * v3 + (1-t) * v4
}

Ps <- matrix(0,(n-max.s+min.s),2)

for(i in (-min.s+1):(n-max.s)){
	s1 <- s[1]+i
	s2 <- s[2]+i
	v1 <- c(a,1)
	v2 <- Xb[s1,]
	v3 <- c(b,1)
	v4 <- Xa[s2,]
	Ps[i,] <- my.cross.2.seg(v1,v2,v3,v4)
}

for(i in 1:(length(Ps[,1])-1)){
	segments(Ps[i,1],Ps[i,2],Ps[i+1,1],Ps[i+1,2])
}