検算〜２変量常微分方程式と複比の関係

• 適当に行列を作ってやってみる

my.matrix.eigen <- function(lambdas,vs){
  Vs <- t(t(vs) * lambdas)
	Vs %*% solve(vs)
}

exp.m <- function(A,n){
  # 固有値分解
	eigen.out<-eigen(A)
	# P=V,P^{-1}=U
	V<-eigen.out[[2]]
	U<-solve(V)
	B<-diag(exp(eigen.out[[1]]*n))
	#B <- diag(eigen.out[[1]]^n)
	X <- V%*%B%*%U
	return(list(matrix = X, eigen.vs <- eigen.out[[1]]))
}

my.doubleratio <- function(x){
	if(!is.matrix(x)){
		x <- matrix(x,nrow=length(x))
	}
	P <- x[1:(length(x[,1])-3),]
	Q <- x[4:length(x[,1]),]
	S <- x[2:(length(x[,1])-2),]
	R <- x[3:(length(x[,1])-1),]
	((P-R)/(Q-R))/((P-S)/(Q-S))
}
n.iter <- 50
dr.calcs.min <- dr.calcs.max <- drs <- rep(0,n.iter)

for(ii in 1:n.iter){
	lambdas <- c(runif(1),runif(1)*3)
	vs <- matrix(rnorm(4)*10,2,2)
	A <- my.matrix.eigen(lambdas,vs)
	# 等間隔なt
	t <- seq(from=-5,to=5,length=20)
	X <- matrix(0,length(t),length(A[,1]))
	X.init <- runif(2)
	for(i in 1:length(t)){
	  X[i,] <- exp.m(A,t[i])[[1]] %*% X.init
	}
	x <- X[,1]/X[,2]
	plot(Re(x))
	dr.calc <- my.doubleratio(x)

	delta <- t[2]-t[1]
	k1 <- lambdas[1]
	k2 <- lambdas[2]
	delta.k <- k1-k2
	dr <- (exp(delta.k/2*delta) + exp(-delta.k/2*delta))^2
	dr.calcs.min[ii] <- min(dr.calc)
	dr.calcs.max[ii] <- max(dr.calc)
	drs[ii] <- dr
}

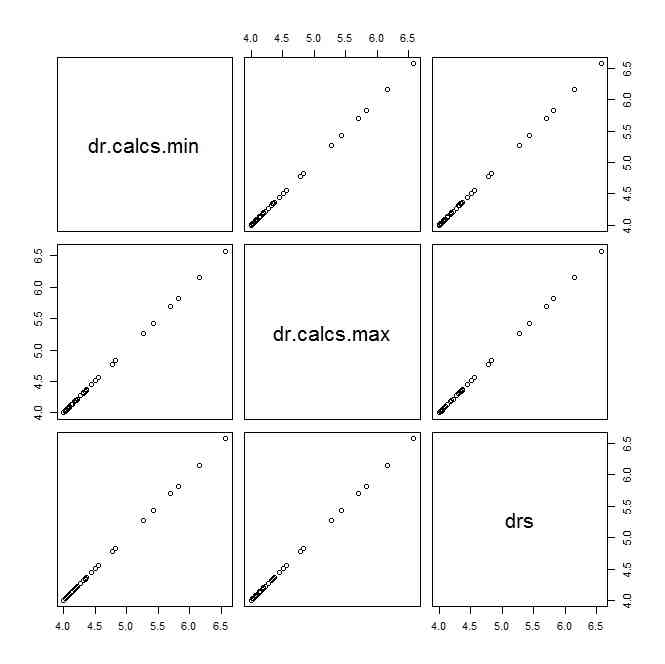
plot(data.frame(dr.calcs.min,dr.calcs.max,drs))