ボロノイ図・ドロネー図 - ryamadaのコンピュータ・数学メモ

空間に点がばらまかれているときに、その点を頂点とする単体(三角形の一般次元化したもの)の敷き詰めとするのがドロネー図作成
二次元でやれば

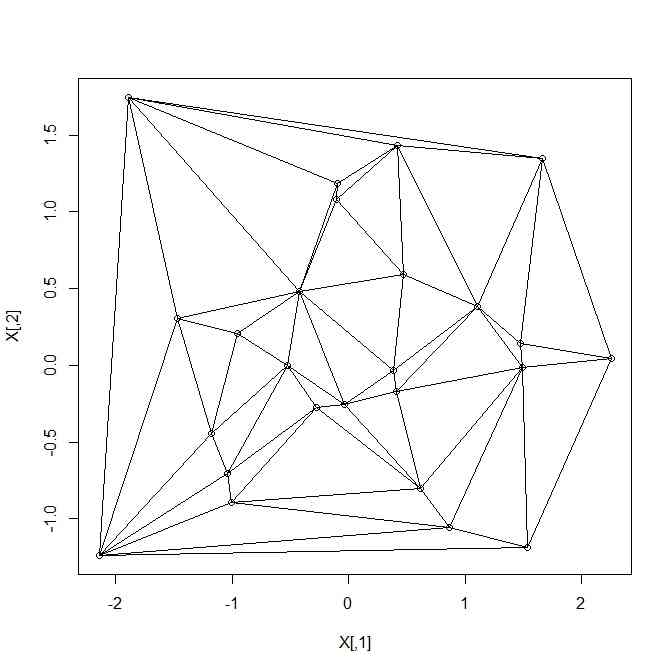
library(geometry)
X <- matrix(rnorm(50),ncol=2)
delaunay.X <- delaunayn(X)
plot(X)
delaunay.X.2 <- rbind(delaunay.X[,1:2],delaunay.X[,2:3],delaunay.X[,c(3,1)])
segments(X[delaunay.X.2[,1],1],X[delaunay.X.2[,1],2],X[delaunay.X.2[,2],1],X[delaunay.X.2[,2],2])

各点が空間に占める支配領域で考えると、このドロネー図の各線分の垂直二等分線を引いて区画する方法があって、そのようにして支配領域を定めた図がボロノイ図
支配領域の広さを考えるなら、ボロノイ図における支配面積が適当だ
が、ドロネー図とボロノイ図とでは情報量が違う
ドロネー図は点の座標とn次元空間にあるn+1頂点を持つn単体の頂点座標IDの組で情報のすべてになるが
ボロノイ図では、国境を構成する点の数が増えるので、情報量が増える
ドロネー図における、「ある点を含む単体の体積の総和」を「各点の周りの体積」とみなすことにすれば、計算はずいぶん軽くなる
ちなみに、n次元空間にある頂点数n+1の単体の体積は、そのn+1本の長さnのベクトルのうちの１本のベクトルについて、残りのn本のベクトルから、この１本のベクトルを引いたベクトルを取り出し、それが作るnxn行列を作れば、体積はそのnxn行列のdeterminantに $\frac{1}{n!}$ を掛けたもの、と言う簡単なものになっている(こちら)

# Determinantを使って体積を計算する
my.simplex.volume <- function(V,factorial=FALSE){
	n <- length(V[1,])
	K <- matrix(V[1:n,],ncol=n)
	K. <- t(K)-V[n+1,]
	if(factorial){
		return(det(K.)/factorial(n))
	}else{
		return(det(K.))
	}
	
}
# ドロネー単体頂点IDのセットを求める
delaunay.X <- delaunayn(X)
# 頂点座標の行列Xと頂点IDベクトルaとから単体体積を計算する関数
my.delaunay.vol <- function(a,X){
	tmp <- matrix(X[a,],ncol=length(X[1,]))
	my.simplex.volume(tmp)
}
# すべてのドロネー単体体積を計算
spx.vol <- apply(delaunay.X,1,my.delaunay.vol,X)
# すべての点について周辺ドロネー単体体積を加算
Vol <- rep(0,length(X[,1]))
for(i in 1:length(Vol)){
	tmp <- (delaunay.X==i)
	tmp.2 <- apply(tmp,1,any)
	Vol[i] <- sum(abs(spx.vol[which(tmp.2)]))
}

ドロネー単体ができると、その内部が外部かを判定したくなる
- n次元のn+1頂点のうち１頂点を基準として、それが張っている「三角錐」の内部の点は、そのn本のベクトルの線形和で表され、係数はすべて非負でかつ、係数の和は１以下、それが内部と表面。

# n次元空間でn単体内かどうかの判定
judge.inside <- function(x,V){
	n <- length(x)
	K <- matrix(V[1:n,],ncol=n)
	K. <- t(K)-V[n+1,]
	tmp <- solve(K.,x-V[n+1,])
	all(tmp>=0 & sum(tmp)<=1)
}

V <- matrix(c(1,0,0,0,1,0,0,0,1,-1,-1,-1),byrow=TRUE,ncol=3)
xx <- matrix(runif(30000,min=-1,max=1),ncol=3)

tf <- apply(xx,1,judge.inside,V)
plot3d(xx[which(tf),])

どのドロネー三角形の内部かがわかったら、その頂点ベクトルを使って線形和でその点を表したい

# delaunay.Xとその頂点値から任意の座標の値を出す
my.linear.delaunay <- function(v,X,delaunay.X,Y.post){
	inside. <- t(apply(delaunay.X,1,my.judge.inside.ID,X,v))
	#print(inside.)
	inside.ID <- which(inside.[,1]==1)
	#print(inside.[inside.ID,])

	inside.coef <- inside.[inside.ID,2:length(inside.[inside.ID,])]
	tmp <- c(inside.coef,1-sum(inside.coef))
	print(tmp)
	print(Y.post[delaunay.X[inside.ID,]])
	print(X[delaunay.X[inside.ID,]])
	sum(tmp*Y.post[delaunay.X[inside.ID,]])
}

- これを使ったRソースのメモ

# 単体の体積
my.simplex.volume <- function(V,factorial=FALSE){
	n <- length(V[1,])
	K <- matrix(V[1:n,],ncol=n)
	K. <- t(K)-V[n+1,]
	if(factorial){
		return(det(K.)/factorial(n))
	}else{
		return(det(K.))
	}
	
}

# 単体の体積計算をドロネー頂点ID情報で行うための関数
my.delaunay.vol <- function(a,X){
	tmp <- matrix(X[a,],ncol=length(X[1,]))
	my.simplex.volume(tmp)
}
# n次元空間でn単体内かどうかの判定
judge.inside <- function(x,V){
	n <- length(x)
	K <- matrix(V[1:n,],ncol=n)
	K. <- t(K)-V[n+1,]
	tmp <- solve(K.,x-V[n+1,])
	judge <- all(tmp>=0 & sum(tmp)<=1)
	return(c(as.numeric(judge),tmp))
}

V <- matrix(c(1,0,0,0,1,0,0,0,1,-1,-1,-1),byrow=TRUE,ncol=3)
xx <- matrix(runif(30000,min=-1,max=1),ncol=3)

tf <- apply(xx,1,judge.inside,V)
plot3d(xx[which(tf),])

my.rw.density.mx <- function(X,Y,n,r){
	D <- as.matrix(dist(X))
	D.e <- exp(-D^2)
	diag(D.e) <- 0

	D.e.2 <- D.e/apply(D.e,1,sum)
	diag(D.e.2) <- r
	D.e.2 <- D.e.2/apply(D.e.2,1,sum)
	eigen.out <- eigen(t(D.e.2))
	V <- eigen.out[[2]]
	S <- diag(eigen.out[[1]]^n)
	U <- solve(V)
	V%*%S%*%U
}

# Xは観測点座標行列、n,rは酔歩平滑化のためのパラメタ
my.delaunay.rw.density <- function(X,n=1000,r=0.1){
	# 点の数
	n.pt <- length(X[,1])
	# ドロネー化(１次元の場合は、大小隣の点と結び合う線分が指定される)
	delaunay.X <- delaunayn(X)
	# ドロネー三角形(の一般次元化)体積を計算
	# １次元の場合は線分長
	spx.vol <- apply(delaunay.X,1,my.delaunay.vol,X)
	spx.per.v <- list()
	# 各観察点の「ドロネー的体積」
	Vol <- rep(0,n.pt)
	for(i in 1:n.pt){
		tmp <- (delaunay.X==i)
		tmp.2 <- apply(tmp,1,any)
		spx.per.v[[i]] <- which(tmp.2)
		Vol[i] <- sum(abs(spx.vol[which(tmp.2)]))
	}
	# length(X[1,])+1回ずつ数えているので
	Vol <- Vol/(length(X[1,])+1)
	# 「ドロネー的体積」で除することで、１観察の空間的重みに換算する
	Y.d <- 1/Vol
	#Y.d <- Y.d/sum(Y.d)*n.pt
	# 酔歩による平滑化をこの「ドロネー的体積補正」した後の観測状態に実施する
	RW.Mx.d <- my.rw.density.mx(X,Y.d,n,r)
	# 平滑化後の各点の重み
	Y.post <- RW.Mx.d %*% Y.d
	# Volは各点のドロネー的体積、Y.dはその逆数。各点での密度に相当
	# Y.postは平滑化後の各点の重み
	# Mは平滑のための行列(指数行列処理にて酔歩平衡状態での移動行列)
	# 配分した重みにより、各ドロネー三角の重みを計算
	spx.weight <- rep(0,length(delaunay.X[,1]))
	for(i in 1:n.pt){
		tmp <- spx.per.v[[i]]
		#print(tmp)
		#print(sum(abs(spx.vol[tmp])))
		spx.weight[tmp] <- spx.weight[tmp] + Y.post[i] * Vol[i]*abs(spx.vol[tmp])/sum(abs(spx.vol[tmp]))
	}
	return(list(Vol=Vol,Y.d=Y.d,Y.post=Y.post,M = RW.Mx.d,delaunay.X = delaunay.X,spx.vol=spx.vol,spx.weight=spx.weight))
}
# 
my.judge.inside.ID <- function(a,X,v){
	tmp <- as.matrix(X[a,],ncol=length(X[1,]))
	#print(tmp)
	judge.inside(v,tmp)
}
# delaunay.Xとその頂点値から任意の座標の値を出す
my.linear.delaunay <- function(v,X,delaunay.X,Y.post){
	inside. <- t(apply(delaunay.X,1,my.judge.inside.ID,X,v))
	#print(inside.)
	inside.ID <- which(inside.[,1]==1)
	#print(inside.[inside.ID,])

	inside.coef <- inside.[inside.ID,2:length(inside.[inside.ID,])]
	tmp <- c(inside.coef,1-sum(inside.coef))
	print(tmp)
	print(Y.post[delaunay.X[inside.ID,]])
	print(X[delaunay.X[inside.ID,]])
	sum(tmp*Y.post[delaunay.X[inside.ID,]])
}
# １次元の分布
# 母分布を決めよう
means <- c(0,0)
sds <- c(1,1)
ratio <- c(0.4,0.6)
N.pt <- 50
X <- c(rnorm(N.pt*ratio[1],means[1],sds[1]),rnorm(N.pt*ratio[2],means[2],sds[2]))
true.Dens <- ratio[1] * dnorm(X,means[1],sds[1])+ratio[2]*dnorm(X,means[2],sds[2])
# 行列型にする
X <- matrix(X,ncol=1)
# 各点に１観測ずつ
Y <- rep(1,length(X[,1]))

# 酔歩による平滑化をこの「ドロネー的体積補正」する前とした後の観測状態に実施するn <- 1000
r <- 0.0001
RW.Mx <- my.rw.density.mx(X,Y,n,r)
# 平滑化後の各点の重み
Z <- RW.Mx %*% Y

# ドロネー的体積補正法
D.out <- my.delaunay.rw.density(X,n,r)
Z.d <- D.out$Y.post

dens.X <- density(X,bw = "SJ-ste")
plot(dens.X,lwd=3)
ord <- order(X)
points(X[ord],Z[ord]/max(Z)*max(dens.X[[2]]),pch=20,col=2,type="b")
points(X[ord],Z.d[ord]/max(Z.d)*max(dens.X[[2]]),pch=20,col=3,type="b")
points(X[ord],true.Dens[ord]/max(true.Dens)*max(dens.X[[2]]),pch=20,col=4,type="l",lwd=3)


# １次元の分布
# 母分布を決めよう
means <- c(0,3)
sds <- c(1,1)
ratio <- c(0.4,0.6)
N.pt <- 200
X <- c(rnorm(N.pt*ratio[1],means[1],sds[1]),rnorm(N.pt*ratio[2],means[2],sds[2]))
true.Dens <- ratio[1] * dnorm(X,means[1],sds[1])+ratio[2]*dnorm(X,means[2],sds[2])
# 行列型にする
X <- matrix(X,ncol=1)
# 各点に１観測ずつ
Y <- rep(1,length(X[,1]))

# 酔歩による平滑化をこの「ドロネー的体積補正」する前とした後の観測状態に実施するn <- 1000
r <- 0.1
RW.Mx <- my.rw.density.mx(X,Y,n,r)
# 平滑化後の各点の重み
Z <- RW.Mx %*% Y

# ドロネー的体積補正法
D.out <- my.delaunay.rw.density(X,n,r)
Z.d <- D.out$Y.post

dens.X <- density(X,bw = "SJ-ste")
plot(dens.X,lwd=3)
ord <- order(X)
points(X[ord],Z[ord]/max(Z)*max(dens.X[[2]]),pch=20,col=2,type="b")
points(X[ord],Z.d[ord]/max(Z.d)*max(dens.X[[2]]),pch=20,col=3,type="b")
points(X[ord],true.Dens[ord]/max(true.Dens)*max(dens.X[[2]]),pch=20,col=4,type="l",lwd=3)

# １次元の分布
# 母分布を決めよう
means <- c(0,10)
sds <- c(1,1)
ratio <- c(0.4,0.6)
N.pt <- 200
X <- c(rnorm(N.pt*ratio[1],means[1],sds[1]),rnorm(N.pt*ratio[2],means[2],sds[2]))
true.Dens <- ratio[1] * dnorm(X,means[1],sds[1])+ratio[2]*dnorm(X,means[2],sds[2])
# 行列型にする
X <- matrix(X,ncol=1)
# 各点に１観測ずつ
Y <- rep(1,length(X[,1]))

# 酔歩による平滑化をこの「ドロネー的体積補正」する前とした後の観測状態に実施するn <- 1000
r <- 0.1
RW.Mx <- my.rw.density.mx(X,Y,n,r)
# 平滑化後の各点の重み
Z <- RW.Mx %*% Y

# ドロネー的体積補正法
D.out <- my.delaunay.rw.density(X,n,r)
Z.d <- D.out$Y.post

dens.X <- density(X,bw = "SJ-ste")
plot(dens.X,lwd=3)
ord <- order(X)
points(X[ord],Z[ord]/max(Z)*max(dens.X[[2]]),pch=20,col=2,type="b")
points(X[ord],Z.d[ord]/max(Z.d)*max(dens.X[[2]]),pch=20,col=3,type="b")
points(X[ord],true.Dens[ord]/max(true.Dens)*max(dens.X[[2]]),pch=20,col=4,type="l",lwd=3)

# １次元の分布
# 母分布を決めよう
means <- c(0,50)
sds <- c(1,8)
ratio <- c(0.2,0.8)
N.pt <- 500
X <- c(rnorm(N.pt*ratio[1],means[1],sds[1]),rnorm(N.pt*ratio[2],means[2],sds[2]))
true.Dens <- ratio[1] * dnorm(X,means[1],sds[1])+ratio[2]*dnorm(X,means[2],sds[2])
# 行列型にする
X <- matrix(X,ncol=1)
# 各点に１観測ずつ
Y <- rep(1,length(X[,1]))

# 酔歩による平滑化をこの「ドロネー的体積補正」する前とした後の観測状態に実施するn <- 1000
r <- 0.1
RW.Mx <- my.rw.density.mx(X,Y,n,r)
# 平滑化後の各点の重み
Z <- RW.Mx %*% Y

# ドロネー的体積補正法
D.out <- my.delaunay.rw.density(X,n,r)
Z.d <- D.out$Y.post

dens.X <- density(X,bw = "SJ-ste")
#dens.X <- density(X)
plot(dens.X,lwd=3)
ord <- order(X)
points(X[ord],Z[ord]/max(Z)*max(dens.X[[2]]),pch=20,col=2,type="b")
points(X[ord],Z.d[ord]/max(Z.d)*max(dens.X[[2]]),pch=20,col=3,type="b")
points(X[ord],true.Dens[ord]/max(true.Dens)*max(dens.X[[2]]),pch=20,col=4,type="l",lwd=3)



# １次元の分布
# 母分布を決めよう
means <- c(0,2)
sds <- c(1,8)
ratio <- c(0.3,0.7)
N.pt <- 500
X <- c(rnorm(N.pt*ratio[1],means[1],sds[1]),rnorm(N.pt*ratio[2],means[2],sds[2]))
true.Dens <- ratio[1] * dnorm(X,means[1],sds[1])+ratio[2]*dnorm(X,means[2],sds[2])
# 行列型にする
X <- matrix(X,ncol=1)
# 各点に１観測ずつ
Y <- rep(1,length(X[,1]))

# 酔歩による平滑化をこの「ドロネー的体積補正」する前とした後の観測状態に実施するn <- 1000
r <- 0.1
RW.Mx <- my.rw.density.mx(X,Y,n,r)
# 平滑化後の各点の重み
Z <- RW.Mx %*% Y

# ドロネー的体積補正法
D.out <- my.delaunay.rw.density(X,n,r)
Z.d <- D.out$Y.post

dens.X <- density(X,bw = "SJ-ste")
#dens.X <- density(X)

xx <- seq(from=min(X),to=max(X),length=20)
Y.xx <- rep(0,length(xx))
for(i in 1:length(xx)){
	Y.xx[i] <- my.linear.delaunay(xx[i],X,D.out$delaunay.X,D.out$Y.post)
}

plot(dens.X,lwd=3)
ord <- order(X)
points(X[ord],Z[ord]/max(Z)*max(dens.X[[2]]),pch=20,col=2,type="b")
points(X[ord],Z.d[ord]/max(Z.d)*max(dens.X[[2]]),pch=20,col=3,type="b")
points(X[ord],true.Dens[ord]/max(true.Dens)*max(dens.X[[2]]),pch=20,col=4,type="l",lwd=3)

points(xx,Y.xx/max(Y.xx)*max(dens.X[[2]]),pch=20,col=5)



# １次元の分布
# 母分布を決めよう
means <- c(0,50)
sds <- c(1,5)
ratio <- c(0.2,0.8)
N.pt <- 100
X <- c(rnorm(N.pt*ratio[1],means[1],sds[1]),rnorm(N.pt*ratio[2],means[2],sds[2]))
true.Dens <- ratio[1] * dnorm(X,means[1],sds[1])+ratio[2]*dnorm(X,means[2],sds[2])
# 行列型にする
X <- matrix(X,ncol=1)
# 各点に１観測ずつ
Y <- rep(1,length(X[,1]))# 酔歩による平滑化をこの「ドロネー的体積補正」する前とした後の観測状態に実施するn <- 1000
r <- 0.1
RW.Mx <- my.rw.density.mx(X,Y,n,r)
# 平滑化後の各点の重み
Z <- RW.Mx %*% Y

# ドロネー的体積補正法
D.out <- my.delaunay.rw.density(X,n,r)
Z.d <- D.out$Y.post

dens.X <- density(X,bw = "SJ-ste")
#dens.X <- density(X)

xx <- seq(from=min(X),to=max(X),length=100)
Y.xx <- rep(0,length(xx))
for(i in 1:length(xx)){
	Y.xx[i] <- my.linear.delaunay(xx[i],X,D.out$delaunay.X,D.out$Y.post)
}

plot(dens.X,lwd=3)
ord <- order(X)
points(X[ord],Z[ord]/max(Z)*max(dens.X[[2]]),pch=20,col=2,type="b")
points(X[ord],Z.d[ord]/max(Z.d)*max(dens.X[[2]]),pch=20,col=3,type="b")
points(X[ord],true.Dens[ord]/max(true.Dens)*max(dens.X[[2]]),pch=20,col=4,type="l",lwd=3)

points(xx,Y.xx/max(Y.xx)*max(dens.X[[2]]),pch=20,col=5)


D.X <- as.matrix(dist(X))
plot(D.out$M,D.X)

my.dirichlet.est.1d <- function(X.obs,X.target=X.obs,Y,Y.level){
	if(length(X.obs)<=1){
		return(list(est=matrix(1/length(Y.level),length(X.target),length(Y.level)),bw=range(X.target)))
	}
	#bw <- density(X.obs)$bw
	bw <- density(X.obs,bw = "SJ-ste")
	ret <- matrix(0,length(X.target),length(Y.level))
	for(i in 1:length(Y.level)){
		s <- which(Y==Y.level[i])
		tmp.X <- X.obs[s]
		X.obs.target <- expand.grid(tmp.X,X.target)
		tmp.d <- dnorm(X.obs.target[,1]-X.obs.target[,2],0,bw)
		tmp.d.m <- matrix(t(tmp.d),length(tmp.X),length(X.target))
		ret[,i] <- apply(tmp.d.m,2,sum)
	}
	return(list(est=ret,bw=bw))
}