2013-07-19

単純なルールでself-avoiding path

先日のMIKUでフラーレン上のエッジを選び方が話題になった
あるルールでエッジを選んでいくと、通り道の途中にぶつかることなく、出発点に戻る(サイクルを作る)ことが必然であることが示された
フラーレンは閉じた空間・有限な空間なので、いつかは通り道のどこかにぶつかるしかなく、「途中にぶつかることを禁止」してエッジを選ぶと結果として出発点に戻るしかない、という論理だった
フラーレンは六角形と五角形とが規則正しく配置して、結果として球面に並ぶ構造で、サッカーボールと同じ

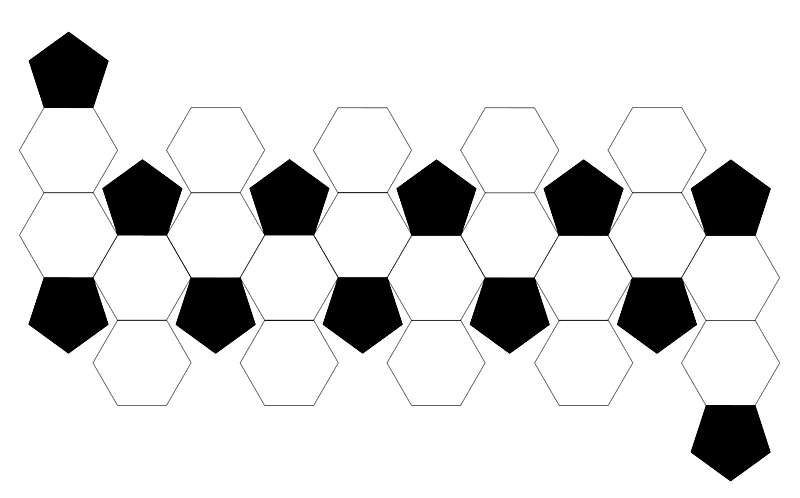
展開図にすると

サッカーボールは３次元で閉じてしまうので、平面にして(無限にもなるのだが)みる。展開図の「黒い五角形」を「(黒い)六角形」にすると、ベンゼン環を敷き詰めた構造と同じになる。しかも、「白い六角形」は３つの二重結合を持つ環で、「黒い六角形」は「穴」であってベンゼン環ではない(これはグラフェン(Wiki記事)

(http://www.org-chem.org/yuuki/planar/planar.htmlより)

グラフェン上をごく単純なルールで酔歩すると、どん詰まりにならずにself-avoiding pathができる。self-avoiding pathは空間探索のやりかたとして餌探しのときなどには有効(なはず)なので、ちょっと面白い

以下、ソース(これをサッカーボール状に丸めたい…→こちら)

# 酔歩の歩数
#n.iter <- 10000 # 掲載図は10000歩
n.iter <- 1000
# 酔歩の座標格納行列
X <- matrix(0,n.iter,2)
# 酔歩の１歩は１重結合か２重結合かの２種類なので、それを記録
# ただし、ルールとして、１重、２重が交互になるように歩く
e.type <- rep(0,n.iter-1)
# １歩のベクトルは６種類ある。その６種類の履歴を格納
e.vector.id <- rep(0,n.iter-1)
# ６種類のベクトルを格納するvs
t <- (seq(from=0,to=1,length=7)*2*pi)[-7]
vs <- cbind(cos(t),sin(t))
# ある一歩の次の一歩は、最後の一歩から左右に30度の２方向のうちのどちらかになる。その最後の一歩と選べる２ベクトルの関係のベクトル
vs.relation <- matrix(0,6,6)
for(i in 1:6){
	for(j in 1:6){
		if(abs(i-j)==1){
			vs.relation[i,j] <- 1
		}
	}
}
vs.relation[1,6] <- vs.relation[6,1] <- 1
vs.relation
# 最初の２歩は決め打ちにする(決め打ちにしても一般性は(ほぼ)失われない)
e.type[1] <- 1
e.type[2] <- 2
e.vector.id[1] <- 1
e.vector.id[2] <- 2
X[2,] <- X[1,] + vs[e.vector.id[1],]
X[3,] <- X[2,] + vs[e.vector.id[2],]
# ３歩目と３歩目が決める４番目の位置から、n.iter番目の位置までを酔歩する
for(i in 4:n.iter){
# 来た時が１重結合だったら、次は２重結合
	if(e.type[i-2]==1){
# 選びうる２つのベクトルのうち、片方は１重結合でもう片方は２重結合になっている(グラフェンの性質から)
# 選べる２ベクトルのうち、１重結合なのは、ひとつ前の１歩のベクトル(それは２重結合だった)と同じベクトルなので、それとは違う方を選ばせる
# つまり、選択の余地はなく、ルールに従ってかならずある方向に進む
		to.select <- which(vs.relation[e.vector.id[i-2],]==1)
		e.type[i-1] <- 2
		e.vector.id[i-1] <- to.select[which(to.select!=e.vector.id[i-3])]
		X[i,] <- X[i-1,] + vs[e.vector.id[i-1],]
# 来た時が２重結合だったら、次は１重結合
	}else{
# １重結合が必ず２本ある
# ２本のうち、どちらかをランダムに選ぶ
# ただし、もし、選んで１歩進んだ先がすでに通った道の上の点ならそれを選ぶのはやめる
# また、選んだ１歩(１重結合)の先の２重結合は決まっているのだから、２歩先も読めて、２歩先がすでに通った道の上の点なら、やはり選ぶのをやめる
# 選ぶのをやめたら、もう片方を選ぶしかない
# 次の１歩の候補ベクトルIDをランダムに選ぶ
		to.select <- sample(which(vs.relation[e.vector.id[i-2],]==1))
		e.type[i-1] <- 1
		tmp.e1 <- to.select[1]
		to.select.2.1 <- which(vs.relation[tmp.e1,]==1)
		tmp.e1.2 <- to.select.2.1[which(to.select.2.1!=e.vector.id[i-2])]
# １歩目、２歩目の座標を仮に計算する
		tmp.X1 <- X[i-1,] + vs[tmp.e1,]
		tmp.X1.2 <- tmp.X1 + vs[tmp.e1.2,]
# １歩目、２歩目の座標と、これまでに通った道の上の点(ただし、出発点を除く)との距離を計算する
		dist1 <- apply((t(t(X[2:(i-1),])-tmp.X1))^2,1,sum)
		dist2 <- apply((t(t(X[2:(i-1),])-tmp.X1.2))^2,1,sum)
# もし同じ点の上に来たら、選択をやめる(ただし、距離が０かどうかで判定すると、計算の誤差でうまく行かないので不等号を使ってある
		if(min(c(dist1,dist2)) > 10^(-4)){
		#if(min(c(dist1,dist2)) != 10^(-4)){
			e.vector.id[i-1] <- to.select[1]
			X[i,] <- tmp.X1
		}else{
			e.vector.id[i-1] <- to.select[2]
			X[i, ] <- X[i-1,] + vs[e.vector.id[i-1],]
		}

	}
# もし、出発点に戻ったなら、処理をやめる
	if(sum((X[1,]-X[i,])^2)==0){
		break;
	}
}
# プロットする
# １重結合は黒、２重結合は赤
xlim <- ylim <- range(X)
plot(X,cex = 100/n.iter,xlim = xlim,ylim=ylim)
for(i in 1:length(e.type)){
	segments(X[i,1],X[i,2],X[i+1,1],X[i+1,2],col=e.type[i])
}