2012-12-04

こんな感じ？確率過程の収束

収束確率収束概収束分布収束平均収束 MIKU

この記事は誤り多数
こちらに概収束と確率収束、平均収束の話がある
他にもいくつか確率変数・確率変数列の収束を説明する用語がある
ごちゃごちゃしている(頭の中が)ので、わかる範囲で整理したい
確率変数と、確率変数列の話である
- 確率変数をX、確率変数列を{ $X_n$ }とすることもあるようだが、すでにX、{ $X_n$ }と似ているので、紛らわしい
- 確率変数をX、確率変数列をSとしてしまう。Sは「変数列」だから、いくつも値が連なったもの
収束の話である
- いくつも「○○収束」と呼び分けられている
- なぜなら、「×の△な収束」を考えたときに、×と△の取り合わせが一通りではないから
- 「収束」は収束だが、相互に異なる、「複数の収束」の話である
『Stochastic convergence: 確率過程の？収束』
- 参考(こちら)
- いろいろな確率過程の収束 various possible modes of stochastic convergence
  - 確率密度分布がある値に収束(概収束) Almost sure convergence
  - 起きにくくなるという収束(確率収束) Convergence in probability
  - 観察される確率変数列が分布へと収束(分布収束) Convergence in distribution
  - r-次平均の収束(r-次平均収束) Convergence in r-th order mean
「確率変数列が確率分布へと収束する」話。『分布収束』Convergence in distribution
- 2項分布が正規分布に分布収束する
  - 表裏が等確率で出るコインを投げ続けて表(0)、裏(1)を記録する。今、n回投げて、表が出た回数がk=0,1,2,...,n回になる確率( $S=\{s_0,s_1,...,s_n\}$ を考えよう。
  - $\frac{n!}{k!(n-k)!} \frac{1}{2^n}$ がその確率で、これを2項分布と言う
  - nを大きくしていくとこの二項分布は正規分布に近づいていく
  - これを「正規分布への分布収束」と言う
  - 確率分布である二項分布が確率分布である正規分布に分布収束している
- 別の分布収束
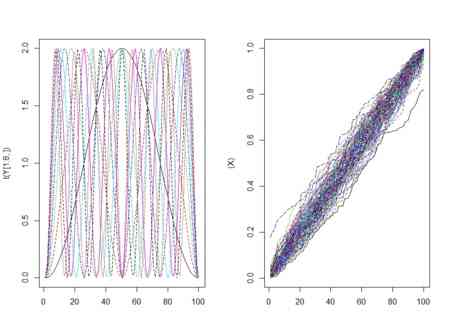
  - $f_n(x) = 1-2\cos(2\pi n x); 0 \le x \le 1$ なる確率密度関数があるとする。これは、nが大きくなるにつれ、0-1区間でどんどん細かいコサインカーブを0-2の間で描くような分布である。どんどんnを大きくしていくと、どんどん上下振動が細かくなり、0-1区間のどこも同一の確率になる。それは0-1区間の一様分布と同等となる。したがって、このような確率密度分布から得る値の列は、0-1区間の一様分布からのそれと同様になる。しかしながら、確率密度関数がまったく一致しないことは言うまでもない
  - 以下に、この確率密度関数の様子を描くとともに、その確率密度関数から取った値列をソートしてプロットしたものを示す
  - このように結果として確率変数の列が同一になっていく、ので、 $f_n(x) = 1-2\cos(2\pi n x); 0 \le x \le 1$ に従う確率変数列は一様分布に分布収束するという
  - 逆に言うと、「確率変数の列S」が分布収束するとは、累積分布関数が収束することであり、累積分布関数が収束するからといって、確率密度関数が収束するわけではないこともわかる
- 確率密度分布がどうなっているのか、まったく気にしないけれど、得られる確率変数列の分布が収束するような収束の仕方のこと

ns <- 1:100
n.pt <- 100
s <- seq(from=0,to=1,length=100)
X <- matrix(0,length(ns),n.pt)
Y <- matrix(0,length(ns),length(s))
for(i in seq(ns)){
	Y[i,] <- 1-cos(2*pi*ns[i]*s)
	cnt <- 1
	while(cnt <= n.pt){
		r <- runif(1)
		r2 <- runif(1)*2
		if(r2<=(1-cos(2*pi*ns[i]*r))){
			X[i,cnt] <- r
			cnt <- cnt +1
		}
	}
}
par(mfcol=c(1,2))
matplot(t(Y[1:8,]),type="l")

X <- apply(X,1,sort)
matplot((X),type="l")

確率密度分布がある値に収束(概収束) Almost sure convergence
- $\lim_{n \to \infty} Pr(X_n = f(n)) =1$
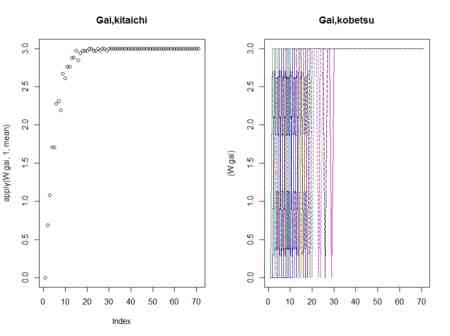
- nが大きくなるとn番目の確率変数がf(n)ばかりを取るようになる、と書いてある
- ここで、f(n)はnの関数であるから、それが定数である場合もあるし、nの関数で変動することもある
- $f(n)=3$ だとして、その確率が $1-\frac{1}{n}$ であって、それ以外の値0を取る確率が $\frac{1}{n}$ であるような場合は、そのような例

Gai.syuusoku.rei <- function(ns,X=1,n.iter = 100){
	p <- 1/(ns)
	W <- matrix(0,length(ns),n.iter)
	for(i in seq(ns)){
		W[i,] <- sample(c(0,X),n.iter,prob=c(p[i],1-p[i]),replace=TRUE)
	}
	W
}
ns <- 10^(seq(from=0,to=7,by = 0.1))
W.gai <- Gai.syuusoku.rei(ns,X=3)
plot(apply(W.gai,1,mean),main ="Gai,kitaichi")
matplot((W.gai),type="l",main ="Gai,kobetsu")

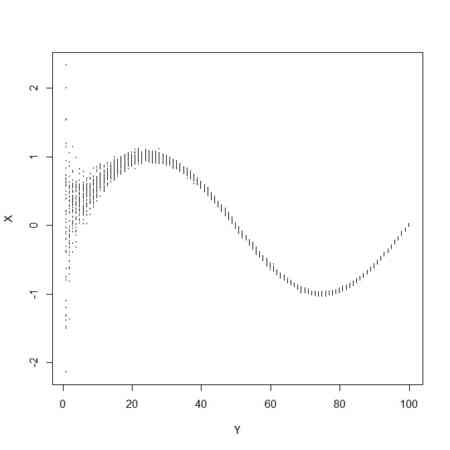
- $f(n)$ が変動する場合はどうだろう
- nが大きくなるにつれて、分散が $\frac{1}{n^2}$ と小さくなりつつ、平均は三角関数で振動するような例の場合は、 $\lim_{n \to \infty} Pr(X_n = f(n)=sin(n*pi/k)) = 1$ ではあるけれども、確率変数列自体はいつまでたっても振動する

n.max <- 100
n <- 1:n.max
k <- 50
m <- sin(n*pi/k)
v <- 1/n^2

n.iter <- 50

X <- matrix(0,n.iter,n.max)
for(i in 1:n.max){
	X[,i] <- rnorm(n.iter,m[i],sqrt(v[i]))
}
Y <- rep(1:n.max,each=n.iter)
plot(Y,X,cex = 0.1)

起きにくくなるという収束(確率収束) Convergence in probability
- 式を見よう
- $\forall \epsilon > 0, \lim_{n \to \infty} Pr(|X_n -a| > \epsilon) = 0$
- どんな正の数 $\epsion$ を取っても、十分に $n$ を大きくとると値aからのずれが $\epsilon$ 以下になる確率がどんどん小さくなって0に近づく
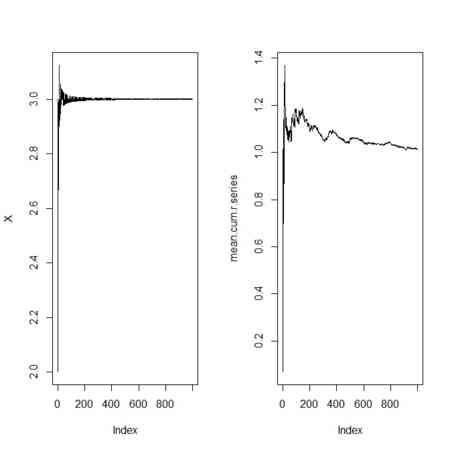
- 今、あるnについて(a,a+1/n,a-1/n)のいずれかしか取らないとすれば、ある $\epsilon$ について $n > \frac{1}{\epsilon}$ を取れば、 $X_n > a+\epsilon, X_n < a-\epsilon$ の確率は0だから確率収束している
- こんな人工的なものではなく、ある期待値を持つ確率変数の列Sを作って、その平均を追いかけていけば、その値はもとの確率変数の期待値にどんどん近づいていく。これも同様の挙動
- これが確率収束

par(mfcol=c(1,2))
n.iter <- 1000
X <-rep(0,n.iter)
a <- 3
for(i in 1:n.iter){
	X[i] <- sample(c(a,a+1/i,a-1/i),1,prob = c(1/3,1/3,1/3))
}

plot(X,type="l")
n.iter <- 1000
r.series <- rexp(n.iter)
cum.r.series <- cumsum(r.series)
mean.cum.r.series <- cum.r.series/seq(r.series)
plot(mean.cum.r.series,type="l")

r-次平均の収束(r-次平均収束) Convergence in r-th order mean
- 確率変数列のr-次モーメントがそれぞれ収束しているかどうかを調べてみよう、といった発想からの収束
確率変数列に関する複数の収束の間の関係
- 概収束するなら確率収束する
- 確率収束するなら分布収束する
- (r+1)-次平均収束するならr-次平均収束する
- １次平均収束するなら確率収束する
- 確率収束するなら、その確率変数列の部分列に概収束するものがある(確率収束がf(n)に収束していても…)
- 分布収束が定数への分布収束なら、確率収束する
- 基本的な関係はWikiの絵で→こちら