球を２つに分ける - ryamadaのコンピュータ・数学メモ

選択公理というのがある
それに関連してバナッハ=タルスキーのパラドクスというのがある
球を２つに分ける話
- 分けるからには、ある点はどちらか片方の球にしか属していなくて
- ２つに分けたそれぞれは球である
- これは、バナッハ=タルスキーのパラドクスの本質的な部分を一部、欠いた説明とも言えるけれど、「この世」にバナッハ=タルスキーのパラドクスを応用しようとすれば、まあ、こんな感じで考えておいてもよいだろう
球にある回転を繰り返すこと
- 球を回転するとき、１回の回転で回る角度がちょうどよければ、何回か回転すると、ちょうど元に戻る
- 角度がちょうどよくないと、永遠に元に戻らない
- 角度の単位に $\pi$ という無理数があるので、有理数な角度の回転の繰り返しは「ちょうどよくない」方に属する
球面は２次元なので、回転を組み合わせる
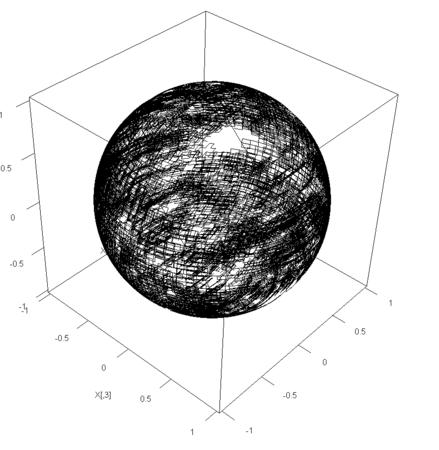
- １種類の回転を続けると、ある点は、球面に１本の軌道を作り、それは円になる
- 球面は２次元なので、２つの異なる回転を「２次元酔歩」すると、球面を覆う酔歩軌道が描ける

# 2種類の回転
# その角度は有理数とする
a <- 0.05
b <- 0.08
# 簡単のためにz軸を軸とした回転aと、y軸を軸とした回転bとを作る
# その回転行列
Ma <- matrix(c(cos(a),-sin(a),0,sin(a),cos(a),0,0,0,1),byrow=TRUE,3,3)
Mb <- matrix(c(cos(b),0,-sin(b),0,1,0,sin(b),0,cos(b)),byrow=TRUE,3,3)

# z軸の周りに正・逆２方向の回転を、y軸の周りにも２方向の回転をさせる
# a,-a,b,-bとする
# それぞのの回転行列をリストに納める

Ms <- list()
Ms[[1]] <- Ma
Ms[[2]] <- t(Ma)
Ms[[3]] <- Mb
Ms[[4]] <- t(Mb)

# 2次元酔歩をさせよう
# 4種類の「一歩」があり得るので、それを作る
s <- sample(1:4,100000,replace=TRUE)

# 回転軸を共有する正・逆回転が続くとそれは「不動」なので、そのような２歩を除く
# この処理はしなくても、軌道的には問題ないが、「自由群」的には、ないことを持ち込む必要があるので、そのようにする
s.2 <- c(s[1])
	for(i in 2:length(s)){
		tmp <- FALSE
		if(s[i-1] ==1){
			if(s[i] != 2){
				tmp <- TRUE
			}
		}else if(s[i-1] == 2){
			if(s[i] != 1){
				tmp <- TRUE
			}
		}else if(s[i-1] ==3){
			if(s[i] != 4){
				tmp <- TRUE
			}
		}else{
			if(s[i] != 3){
				tmp <- TRUE
			}
		}
		if(tmp) s.2 <- c(s.2,s[i])
	}

length(s)-length(s.2)

s <- s.2

# 単位球表面にランダムに点を選び、そこから、酔歩させる
X <- matrix(0,length(s)+1,3)

X[1,] <- runif(3)
X[1,] <- X[1,]/sqrt(sum(X[1,]^2))

for(i in 2:length(X[,1])){
	X[i,] <- Ms[[s[i-1]]] %*% X[i-1,]
}

library(rgl)

X <- rbind(X,diag(rep(1,3)),diag(rep(-1,3)))

plot3d(X,type="l")

２つに分けられることと自由群
- {a,-a,b,-b}が作るすべての配列であって、a -> (-a) という連続と、その逆の(-a) -> aという連続、同様に b -> (-b), (-b) -> bという連続は縮めて、除いてしまう、というルールで配列を作るとする
- a,-a,b,-bをそれぞれ回転として考えれば、正・逆の回転が続いたら、何もなかったことにしても同じだが、それに対応する手続きである
- このような配列を考える

ss <- list()

for(ii in 1:5){

s <- sample(c("a","-a","b","-b"),10,replace=TRUE)

# 回転軸を共有する正・逆回転が続くとそれは「不動」なので、そのような２歩を除く
# この処理はしなくても、軌道的には問題ないが、「自由群」的には、ないことを持ち込む必要があるので、そのようにする
s.2 <- c(s[1])
for(i in 2:length(s)){
	if(s[i] != s.2[length(s.2)]) s.2 <- c(s.2,s[i])
}
length(s)-length(s.2)

s <- s.2

ss[[ii]] <-paste(s,collapse = ":")
}

ss

[[1]]
[1] "-b:-a:a:b:-a:b:-a"

[[2]]
[1] "a:-b:a:-b:b:-a:a"

[[3]]
[1] "-a:b:-b:a:-b:-a:a:b"

[[4]]
[1] "-a:-b:b:a:-a:-b:-a:b:-a"

[[5]]
[1] "-b:b:-a:b:-a:a:-a:b"

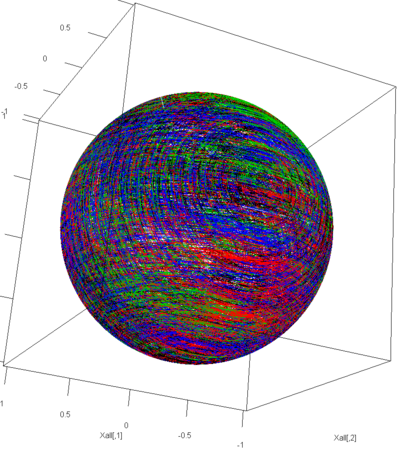
- これはまず、４種類に分けられる。それは、最初がa,-a,b,-bの４つのうちのいずれであるかでの分類である
  - これらを $S(a),S(-a),S(b),S(-b)$ と書くことにする
  - 絵を描こう

# 2次元酔歩をさせよう
# 4種類の「一歩」があり得るので、それを作る
a <- 0.1
b <- 0.1
# 簡単のためにz軸を軸とした回転aと、y軸を軸とした回転bとを作る
# その回転行列
Ma <- matrix(c(cos(a),-sin(a),0,sin(a),cos(a),0,0,0,1),byrow=TRUE,3,3)
Mb <- matrix(c(cos(b),0,-sin(b),0,1,0,sin(b),0,cos(b)),byrow=TRUE,3,3)

# z軸の周りに正・逆２方向の回転を、y軸の周りにも２方向の回転をさせる
# a,-a,b,-bとする
# それぞのの回転行列をリストに納める

Ms <- list()
Ms[[1]] <- Ma
Ms[[2]] <- t(Ma)
Ms[[3]] <- Mb
Ms[[4]] <- t(Mb)

X0 <- runif(3)
X0 <- X0/sqrt(sum(X0^2))
Xall <- matrix(c(1,1,1,-1,-1,-1),byrow=TRUE,nrow=2)
cols <- rep(0,2)
n.iter <- 12
n.step <- 10000
for(ii in 1:n.iter){
	s <- sample(1:4,n.step,replace=TRUE)
	s[1] <- ii %% 4 +1
	tobeavoid <- c(2,1,4,3)
	s[2] <- sample((1:4)[-tobeavoid[s[1]]],1)
	s[3] <- sample((1:4)[-tobeavoid[s[2]]],1)

	
	# 回転軸を共有する正・逆回転が続くとそれは「不動」なので、そのような２歩を除く
	# この処理はしなくても、軌道的には問題ないが、「自由群」的には、ないことを持ち込む必要があるので、そのようにする
	s.2 <- c(s[1])
	for(i in 2:length(s)){
		tmp <- FALSE
		if(s[i-1] ==1){
			if(s[i] != 2){
				tmp <- TRUE
			}
		}else if(s[i-1] == 2){
			if(s[i] != 1){
				tmp <- TRUE
			}
		}else if(s[i-1] ==3){
			if(s[i] != 4){
				tmp <- TRUE
			}
		}else{
			if(s[i] != 3){
				tmp <- TRUE
			}
		}
		if(tmp) s.2 <- c(s.2,s[i])
	}
	length(s)-length(s.2)

	s <- s.2

	# 単位球表面にランダムに点を選び、そこから、酔歩させる
	X <- matrix(0,length(s)+1,3)

	X[1,] <- X0

	for(i in 2:length(X[,1])){
		X[i,] <- Ms[[s[i-1]]] %*% X[i-1,]
	}
	Xall <- rbind(Xall,X)
	cols <- c(cols,0,0,rep(s[1],length(s)+1-3),0)
}

plot3d(Xall,type="l",col=cols)

- この４種類を２種類に分ける方法として、最初がaかそれ以外か、というのもあるだろう
- この２分割が面白いのは、最初がaではない配列は $a S(-a)$ と書けること( $S(-a)$ は初めが-aだが、それにaを付け加えると $S(-a)$ の初めの-aが取れた配列が残るわけだが、 $S(-a)$ の配列の２番目は、-a,b,-bのいずれかであって、aはないからそのようになる
- このことから、次のように言える
  - ある球面上の１点から、ある２つの回転によって定義された折れ線的な軌道を考える
  - 球面は軌道によって覆われる
  - 特に、１ステップが結構な『歩幅』を持つとき、「ぐるりと回っても元の点に戻らない」という性質から、球面はかなりくまなく到達可能である
  - さらに、その軌道は、第１歩が４種類のうちの一つに限定されるので、４種類のそれぞれが、球面をくまなく覆う
  - この４種類は、始点の周辺では、明快に分かれているから、その根っこをぐっと握って、グイと引けば、球面全体をまんべんなく手繰り寄せることができる
  - しかも、４種類のうち１種類を引っ張っても、行き着いている先を「うまく」とって来れば、球面の全体の半分にすることができそうである。「先の付着の仕組み」をうまいことしておけば、ですが(この「うまいこと」が選択公理的な「うまさ」だったり、「点」は、面積がないから、１：３の面積を比較しても、対等とみなすことができるというような「幾何学的なうまさ」だったり。
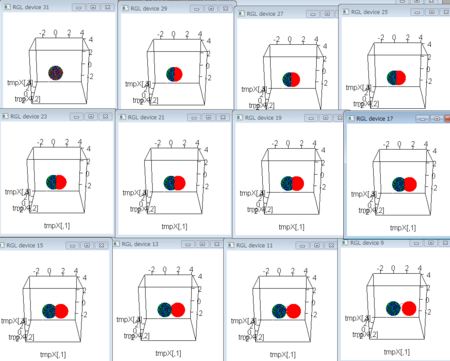
  - 歩幅を粗大にした場合

###########
# 2次元酔歩をさせよう
# 4種類の「一歩」があり得るので、それを作る
a <- 1
b <- 1
# 簡単のためにz軸を軸とした回転aと、y軸を軸とした回転bとを作る
# その回転行列
Ma <- matrix(c(cos(a),-sin(a),0,sin(a),cos(a),0,0,0,1),byrow=TRUE,3,3)
Mb <- matrix(c(cos(b),0,-sin(b),0,1,0,sin(b),0,cos(b)),byrow=TRUE,3,3)

# z軸の周りに正・逆２方向の回転を、y軸の周りにも２方向の回転をさせる
# a,-a,b,-bとする
# それぞのの回転行列をリストに納める

Ms <- list()
Ms[[1]] <- Ma
Ms[[2]] <- t(Ma)
Ms[[3]] <- Mb
Ms[[4]] <- t(Mb)

X0 <- runif(3)
X0 <- X0/sqrt(sum(X0^2))
Xall <- matrix(c(1,1,1,-1,-1,-1),byrow=TRUE,nrow=2)
cols <- rep(0,2)
n.iter <- 12
n.step <- 1000
for(ii in 1:n.iter){
	s <- sample(1:4,n.step,replace=TRUE)
	s[1] <- ii %% 4 +1
	tobeavoid <- c(2,1,4,3)
	s[2] <- sample((1:4)[-tobeavoid[s[1]]],1)
	s[3] <- sample((1:4)[-tobeavoid[s[2]]],1)

	# 回転軸を共有する正・逆回転が続くとそれは「不動」なので、そのような２歩を除く
	# この処理はしなくても、軌道的には問題ないが、「自由群」的には、ないことを持ち込む必要があるので、そのようにする
	s.2 <- c(s[1])
	for(i in 2:length(s)){
		tmp <- FALSE
		if(s[i-1] ==1){
			if(s[i] != 2){
				tmp <- TRUE
			}
		}else if(s[i-1] == 2){
			if(s[i] != 1){
				tmp <- TRUE
			}
		}else if(s[i-1] ==3){
			if(s[i] != 4){
				tmp <- TRUE
			}
		}else{
			if(s[i] != 3){
				tmp <- TRUE
			}
		}
		if(tmp) s.2 <- c(s.2,s[i])
	}
	length(s)-length(s.2)

	s <- s.2

	# 単位球表面にランダムに点を選び、そこから、酔歩させる
	X <- matrix(0,length(s)+1,3)

	X[1,] <- X0

	for(i in 2:length(X[,1])){
		X[i,] <- Ms[[s[i-1]]] %*% X[i-1,]
	}
	Xall <- rbind(Xall,X)
	cols <- c(cols,0,0,rep(s[1],length(s)+1-3),0)
}

plot3d(Xall,type="l",col=cols)

この方式で球から球を引っ張り出してみる

n.t <- 20
kizami <- 0.1
group1 <- which(cols==2)
maxcoord <- n.t * kizami
for(i in 1:n.t){
	tmpX <- Xall
	tmpX2 <- Xall[group1,]
	tmpX2[,1] <- tmpX2[,1]+0.1*i
	tmpX[group1,] <- tmpX2
	tmpX <- rbind(tmpX,rep(maxcoord+1,3),rep(-maxcoord,3))
	plot3d(tmpX,type="l",col=c(cols,rep(0,2)))
	#open3d()
	Sys.sleep(10)
}
for(i in n.t:0){
	tmpX <- Xall
	tmpX2 <- Xall[group1,]
	tmpX2[,1] <- tmpX2[,1]+0.1*i
	tmpX[group1,] <- tmpX2
	tmpX <- rbind(tmpX,rep(maxcoord+1,3),rep(-maxcoord,3))
	plot3d(tmpX,type="l",col=c(cols,rep(0,2)))
	open3d()
	#Sys.sleep(10)
}

library(animation)
saveGIF({
for(i in 1:n.t){
	tmpX <- Xall
	tmpX2 <- Xall[group1,]
	tmpX2[,1] <- tmpX2[,1]+0.1*i
	tmpX[group1,] <- tmpX2
	tmpX <- rbind(tmpX,rep(maxcoord+1,3),rep(-maxcoord,3))
	plot3d(tmpX,type="l",col=c(cols,rep(0,2)))
	

}
},interval=0.05)

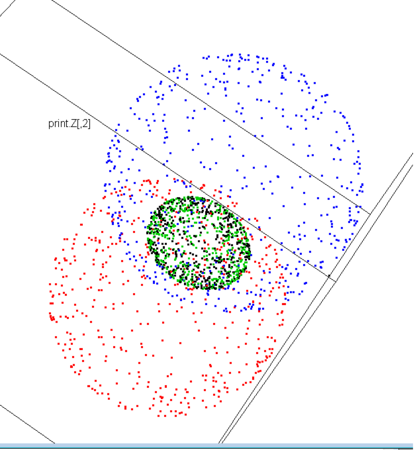
さらに…
- さっさーと動ける要素(切ってはつなぐトポイソメラーゼのようなものがあれば…)もあれば、「滓(おり)」のように残ってしまうものもあるとすると…細胞分裂のcontractile ringのようなものも見えてくる

n.pt <- 1000
X1 <- matrix(rnorm(n.pt*3),ncol=3)
X2 <- matrix(rnorm(n.pt*3),ncol=3)

cols <- c(rep(1,n.pt/2),rep(2,n.pt/2),rep(3,n.pt/2),rep(4,n.pt/2))

Y <- rbind(X1,X2)

Y <- Y/sqrt(apply(Y^2,1,sum))


plot3d(Y,col=cols)

n.t <- 25
kizami <- 0.1
for(i in 0:n.t){
	center1 <- 0
	center2 <- i*kizami
	
	tmp <- Y[1:n.pt,]
	tmp[,1] <- tmp[,1] + kizami*i
	Z <- Y
	Z[1:n.pt,] <- tmp
	
	s1 <- 1:(n.pt/2)
	s2 <- (n.pt+1):(n.pt*3/2)
	
	tmp1 <- Z[s1,]
	tmp2 <- Z[s2,]
	tmp3 <- tmp2
	tmp3[,1] <- tmp3[,1]-i*kizami
	t1 <- which(sqrt(apply(tmp1^2,1,sum))>1)
	t2 <- which(sqrt(apply(tmp3^2,1,sum))>1)
	
	x <- i*kizami/2
	r <- sqrt(1-x^2)
	
	tmp1.1 <- tmp1[t1,]
	tmp1.1[,1] <- x
	tmp1.1[,2] <- tmp1.1[,2]*r
	tmp1.1[,3] <- tmp1.1[,3]*r
	
	tmp1[t1,] <- tmp1.1
	tmp2.1 <- tmp2[t2,]
	tmp2.1[,1] <- x
	tmp2.1[,2] <- tmp2.1[,2]*r
	tmp2.1[,3] <- tmp2.1[,3]*r
	tmp2[t2,] <- tmp2.1
	
	Z[s1,] <- tmp1
	Z[s2,] <- tmp2
	
	print.Z <- rbind(Z,c(3,3,3),c(-1,-1,-1))
	plot3d(print.Z,col=cols)
	Sys.sleep(0.5)
}

繰り返せるように
- 上記のようにしてできた２つの球は、同じ方式でさらに分裂して行ってほしい
- そのときに気になるのは、軌道のセットが、分裂後も分裂前と同様に４方向にバラバラになっていること
  - これは、引っ張るときに使った「根」の部分と、それに続くもう１セグメントを破壊して引き寄せることで達成可能
- また、上記のような球の分裂は、あっち方向にでこっち方向にも起こしたい。それにはすでに対応している
均質性と不均質性
- 上記では、均質な２つの球への分裂が実現できた
- 不均質な分裂も可能だろうか
  - 軌道メッシュの長さが不十分だと、分裂の際に、近傍を中心に引き抜かれる傾向が出る
  - この性質は、極性を持った分裂を表しているかもしれない
  - さらに言えば、メッシュの根っこが少しずつ破壊しながら分裂しているとき、特に分裂頻度が高いとき、メッシュ軌道は徐々に短くなり、特段の仕組みを入れなくても、だんだんに極性を伴った分裂が起きてくることになる
完全再生
- 上の話は、実は、「パラドクス」ではなくて、ただの「(均等)分割」の話
- 本当は「２つの完全な球」を作らなくていけない
- $S(a),S(-a),S(b),S(-b)$ をまず $S(a),S(-a)$ と $S(b),S(-b)$ との２つに分ける
- $S(-a)$ に $a S(-a)$ とすると、 $S(-a),S(b),S(-b)$ となるから、これと $S(a)$ とを合わせると $S(a),S(-a),S(b),S(-b)$ との完全なものができる
- 同様に $S(b),S(-b)$ からも $S(a),S(-a),S(b),S(-b)$ が作れる
- これで「完全な２つの球」にできた(こちらを参照)
- $S(a),S(-a)$ と $S(b),S(-b)$ とに分けるというのは、平面4方向を縦と横とに分けること
- これは中心小体のL字構造(こちらやこちら)と相照らし合っているのでは…(細胞分裂というより染色体分配だけれども)
- では、この分裂後の変換 $a S(-a), b S(-b)$ をやってみよう
- また、分裂後に $-a S(a),a S(-a)$ と $-b S(b),b S(-b)$ をやる、というのも、ありそうな手である。どちらかに限定せずに、最初の回転を除去する、という「全部一斉に」という処理だから
- 後者のやり方の方が、「有限」の軌道の場合には、完全な再生に近い
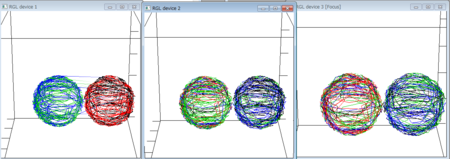
- 図は、左が、分離直後、中央がその後、 $a S(-a),b S(-b)$ のみを実施したもの、右は、 $-a S(a),a S(-a),-b S(b),b S(-b)$ を実施したもの

library(rgl)
###########
# 2次元酔歩をさせよう
# 4種類の「一歩」があり得るので、それを作る
a <- 1
b <- 1
# 簡単のためにz軸を軸とした回転aと、y軸を軸とした回転bとを作る
# その回転行列
Ma <- matrix(c(cos(a),-sin(a),0,sin(a),cos(a),0,0,0,1),byrow=TRUE,3,3)
Mb <- matrix(c(cos(b),0,-sin(b),0,1,0,sin(b),0,cos(b)),byrow=TRUE,3,3)

# z軸の周りに正・逆２方向の回転を、y軸の周りにも２方向の回転をさせる
# a,-a,b,-bとする
# それぞのの回転行列をリストに納める

Ms <- list()
Ms[[1]] <- Ma
Ms[[2]] <- t(Ma)
Ms[[3]] <- Mb
Ms[[4]] <- t(Mb)

X0 <- runif(3)
X0 <- X0/sqrt(sum(X0^2))
Xall <- matrix(c(1,1,1,-1,-1,-1),byrow=TRUE,nrow=2)
s.list <- list()
cols <- rep(0,2)
n.iter <- 12
n.step <- 100
for(ii in 1:n.iter){
	s <- sample(1:4,n.step,replace=TRUE)
	s[1] <- ii %% 4 +1
	tobeavoid <- c(2,1,4,3)
	s[2] <- sample((1:4)[-tobeavoid[s[1]]],1)
	s[3] <- sample((1:4)[-tobeavoid[s[2]]],1)
	
	# 回転軸を共有する正・逆回転が続くとそれは「不動」なので、そのような２歩を除く
	# この処理はしなくても、軌道的には問題ないが、「自由群」的には、ないことを持ち込む必要があるので、そのようにする
	s.2 <- c(s[1])
	for(i in 2:length(s)){
		tmp <- FALSE
		if(s[i-1] ==1){
			if(s[i] != 2){
				tmp <- TRUE
			}
		}else if(s[i-1] == 2){
			if(s[i] != 1){
				tmp <- TRUE
			}
		}else if(s[i-1] ==3){
			if(s[i] != 4){
				tmp <- TRUE
			}
		}else{
			if(s[i] != 3){
				tmp <- TRUE
			}
		}
		if(tmp) s.2 <- c(s.2,s[i])
	}
	length(s)-length(s.2)

	s <- s.2
	s.list[[ii]] <- s
	# 単位球表面にランダムに点を選び、そこから、酔歩させる
	X <- matrix(0,length(s)+1,3)

	X[1,] <- X0

	for(i in 2:length(X[,1])){
		X[i,] <- Ms[[s[i-1]]] %*% X[i-1,]
	}
	Xall <- rbind(Xall,X)
	cols <- c(cols,0,0,rep(s[1],length(s)+1-3),0)
}

plot3d(Xall,type="l",col=cols)

n.t <- 20
kizami <- 0.1
group1 <- which(cols<=2)
maxcoord <- n.t * kizami
for(i in 1:n.t){
	tmpX <- Xall
	tmpX2 <- Xall[group1,]
	tmpX2[,1] <- tmpX2[,1]+kizami*i
	tmpX[group1,] <- tmpX2
	tmpX <- rbind(tmpX,rep(maxcoord+1,3),rep(-maxcoord,3))
	plot3d(tmpX,type="l",col=c(cols,rep(0,2)))
	#open3d()
	Sys.sleep(0.5)
}

# 分離が終わったらS(-a)をa S(-a), S(-b)を b S(-b)しよう

s.list.new <- s.list
for(i in 1:length(s.list.new)){
	if(s.list[[i]][1] ==2) s.list.new[[i]] <- s.list[[i]][-1]
	if(s.list[[i]][1] ==4) s.list.new[[i]] <- s.list[[i]][-1]
}

Xall.new <- matrix(c(1,1,1,-1,-1,-1),byrow=TRUE,nrow=2)
cols.new <- rep(0,2)
for(ii in 1:length(s.list.new)){
	X <- matrix(0,length(s.list.new[[ii]])+1,3)

	X[1,] <- X0

	for(i in 2:length(X[,1])){
		X[i,] <- Ms[[s.list.new[[ii]][i-1]]] %*% X[i-1,]
	}
	if(s.list[[ii]][1] <=2){
		X[,1] <- X[,1] + kizami * n.t
	}
	Xall.new <- rbind(Xall.new,X)
	cols.new <- c(cols.new,0,0,rep(s.list.new[[ii]][1],length(s.list.new[[ii]])+1-3),0)

}
open3d()
tmpX.all <- rbind(Xall.new,rep(maxcoord+1,3),rep(-maxcoord,3))
plot3d(tmpX.all,type="l",col = cols.new)


########
# 全軌道で頭を切り詰めよう
# 分離が終わったらS(-a)をa S(-a), S(-b)を b S(-b)しよう

s.list.new <- s.list
for(i in 1:length(s.list.new)){
	s.list.new[[i]] <- s.list[[i]][-1]
}

Xall.new <- matrix(c(1,1,1,-1,-1,-1),byrow=TRUE,nrow=2)
cols.new <- rep(0,2)
for(ii in 1:length(s.list.new)){
	X <- matrix(0,length(s.list.new[[ii]])+1,3)

	X[1,] <- X0

	for(i in 2:length(X[,1])){
		X[i,] <- Ms[[s.list.new[[ii]][i-1]]] %*% X[i-1,]
	}
	if(s.list[[ii]][1] <=2){
		X[,1] <- X[,1] + kizami * n.t
	}
	Xall.new <- rbind(Xall.new,X)
	cols.new <- c(cols.new,0,0,rep(s.list.new[[ii]][1],length(s.list.new[[ii]])+1-3),0)

}
open3d()
tmpX.all <- rbind(Xall.new,rep(maxcoord+1,3),rep(-maxcoord,3))
plot3d(tmpX.all,type="l",col = cols.new)