1. 線形代数の使い方駆け足で読む『数学をいかに使うか』

駆け足で読む『数学をいかに使うか』の目次はこちら
線形空間
- 体F上の線形空間V。ベクトル空間(こちら)とも言う
- 線形空間Vには次元があってdim(V)と各
- ２つの線形空間V,Wにた対応付けT:V->Wを考えることができて、線形写像と言う
線形写像で次のものを考える
- - 線形空間Vの要素であって、線形写像Tによって、線形空間Wの原点 $0$ に移されるような点が作る空間
  - これは線形空間Vの部分空間
- - 線形空間Vの要素のすべてについて、線形写像によって移した先の線形空間Wの点が作る空間
  - これは線形空間Wの部分空間
- VとWとがどちらも有限次元のとき
  - $dim(T(V))+dim(Ker(T))=dim(V)$
  - $dim(V)=dim(W)$ ならば $Ker(T)=\{0\} \Longleftrightarrow T(V) = W$
多項式・多項式環(こちら)について用いる
- $Ker(T)=\{0\}$ であるということは、 $x,y\in V$ について $Tx=Ty \Longleftrightarrow x=y$
定理1.1.
- $0 \le n \in \mathbf{Z}$ としてn+1個の互いに相違なる実数 $y_0,y_1,...,y_n$ を与え、そのほかにn+1個の実数 $b_0,b_1,...,b_n$ を取る。 $b_0,b_1,...,b_n$ の中には同じものがあってよい。このときn次以下の実数係数の多項式f(x)で、 $\forall i =0,1,...,n, f(y_i)=b_i$ となるものがただ一つ存在する
- これを証明するのに、多項式 $f\in V$ に対して $T(f)=(f(y_0),f(y_1),...,f(y_n))$ と置けば、 $T$ はVからWへの線形写像であるが、 $Ker(T)=\{0\}$ を示すであることが示せるので、それをもってする
- これにより、複数の点を通る多項式を見つけることができる(多項式補完→こちら)
- Rでは多項式のパッケージpolynomを使って、多項式補完することができる

library(polynom)
# y=0を通る点を指定
n<-5
xs<-sample(0:100,n)
pc.out<-poly.calc(xs)
summary(pc.out)
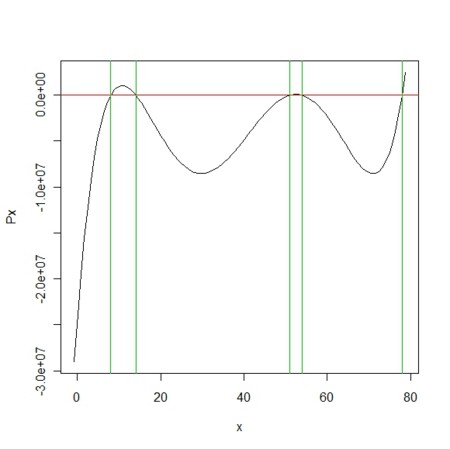
plot(pc.out)
abline(h=0,col=2)
abline(v=xs,col=3)
# (x,y)点を指定
xs<-sample(0:10,n)
ys<-sample(0:10,n)

pc.out2<-poly.calc(xs,ys)
plot(pc.out2)
abline(h=ys,col=2)
abline(v=xs,col=3)

定理1.2.
- 定理1.1. の $y_i,b_i$ のほかにn+1個の実数 $c_0,c_1,...,c_n$ を取る。 $c_0,c_1,...,c_n$ の中には同じものがあってもよい。このとき、 $\forall i =0,1,...,n, f(y_i)=b_i$ , $\forall i =0,1,...,n, f'(y_i)=c_i$ となる2n+1次以下の実係数の多項式fがただ一つ存在する。ただし、 $f'(x)$ は $f$ の導関数である
- これを証明するには、 $T(f)=(f(y_0),...,f(y_n),f'(y_0),...,f'(y_n))$ を定めた上で、 $Ker(T)=\{0\}$ を示せばよい
- 多項式補完の延長で言えば、複数の点を通り、かつその点での微分(差分？)を満足する多項式を見つけることができることになる
これらは、線形写像を行列で考えるとき、行列式が非0であることに引き写すこともできる(こちら)

Ker(T)=\{x\in T | T(x)=0 \}
T(V)=\{Tx| x \in V\}
dim(T(V))+dim(Ker(T))=dim(V)
Ker(T)=\{0\} \Longleftrightarrow T(V) = W

ついでに連立方程式を行列で解くのをRで

# 4x+3y+z=2
# 3x+2y-3z=5
# x-3y-2z=-2
a <- matrix(c(4,3,1,3,2,-3,1,-3,-2), 3,3)       
b <- matrix(c(2,5,-2))                      
solve(a,b)