このペイパーに結び目のJones 多項式と団代数の話がある
その中で、結び目が連分数と関係すること、蛇グラフが連分数と関係すること、その結果として、結び目が蛇グラフと関連することが書かれている
そして蛇グラフは閉曲面上の三角化の団代数と関連することから、結び目不変量であるJones多項式が団代数と関連することが書かれている
ある蛇グラフがあるとき、その頂点のパーフェクトマッチングの場合の数を分子とし、その蛇グラフをちょっと削った蛇グラフの頂点のパーフェクトマッチングの場合の数を分母とした分数が、連分数表現できることが書かれている
その連分数表現は蛇グラフの折れ曲がり方により整数列として表せる
今、整数列 $(a_1,a_2,,,)$ があったときに、それが連分数 $a_1 + \frac{1}{a_2 + \frac{1}{a_3 + ...}}$ という連分数とする
このような連分数を整数列 $(a_1,...)$ から計算したいので、Rでコードにしておく
ただし、計算もしたいが、その値の分数表現 $\frac{p}{q}$ もほしいのでそのような関数を作る

my.cont.frac <- function(as){
	n <- length(as)
	bunsi <- as[n-1] * as[n] + 1
	bunbo <- as[n]
	#print(bunsi)
	#print(bunbo)
	if(n > 2){
		for(i in (n-2):1){
			new.a <- as[i]
			
			new.bunsi <- new.a * bunsi + bunbo
			new.bunbo <- bunsi
			#print(i)
			#print(new.bunsi)
			#print(new.bunbo)
			bunsi <- new.bunsi
			bunbo <- new.bunbo
		}
	}

	return(list(q = bunsi/bunbo,bunsi = bunsi,bunbo = bunbo))
}

as <- c(2,2,-2,-2)

my.cont.frac(as)

ちなみに、蛇グラフがまっすぐな時、 $(2,2,-2,-2,2,2,-2,-2,...)$ となる
これは、分子がフィボナッチ数 $\times (3n-1)$ なる数列(A015448 - OEIS)となり
分母がeven Fibonacci number (フィボナッチ数 $\times (3n)$ )(A014445 - OEIS)となっている

tt0 <- c(2,2)

tt <- c()
v <- c()
bunsis <- bunbos <- c()
for(i in 0:k){
	tt <- c(tt,(-1)^i*tt0)
	tmp <- my.cont.frac(tt)
	v <- c(v,tmp$q)
	bunsis <- c(bunsis,tmp$bunsi)
	bunbos <- c(bunbos,tmp$bunbo)
}

plot(v)

bunsis # 

bunbos # even Fibonacci number

2021-03-18

Zonotope

zonotopeは平行四辺形の多次元版のようなもの
あるベクトル $v_i$ について、係数 $a_i; 0 \le a_i \le 1$ を取ると $a_i v_i$ はline segmentになる
複数のline segmentsのMikowski和, $\sum_{i=1}^k a_i v_i$ がzonotope

n.pt <- 6
d <- 2
vs <- matrix(rnorm(n.pt*d),ncol=d)
#n.r.pt <- 10^4
#r <- matrix(runif(n.pt*n.r.pt),ncol=n.pt)
s <- seq(from=0,to=1,length=6)
r <- as.matrix(expand.grid(s,s,s,s,s,s))
X <- r %*% vs
plot(X)

３次元版

n.pt <- 6
d <- 3
vs <- matrix(rnorm(n.pt*d),ncol=d)
#n.r.pt <- 10^4
#r <- matrix(runif(n.pt*n.r.pt),ncol=n.pt)
s <- seq(from=0,to=1,length=11)
r <- as.matrix(expand.grid(s,s,s,s,s,s))
X <- r %*% vs
library(rgl)
plot3d(X)

2021-03-18

トロピカル幾何、トロピカル曲面

トロピカル代数トロピカル幾何 tropical algebra tropical geometry tropical semiring トロピカル半環

トロピカル代数では、２つの演算、積と和があるが、トロピカル積 $\odot$ は、普通の和、トロピカル和 $\oplus$ は、最大値を取る、というルール
トロピカル多項式 $1 \odot x_1^2 \oplus 1 \odot x_2^2 \oplus 2 \odot x_1 x_2 \oplus 2 \odot x_1 \oplus 2 \odot x_2 \oplus 2$ は
$max(1 + 2 x_1, 1 + 2 x_2, 2 + x_1 x_2, 2 + x_1, 2 + x_2, 2)$
これをRで計算して図示してみる

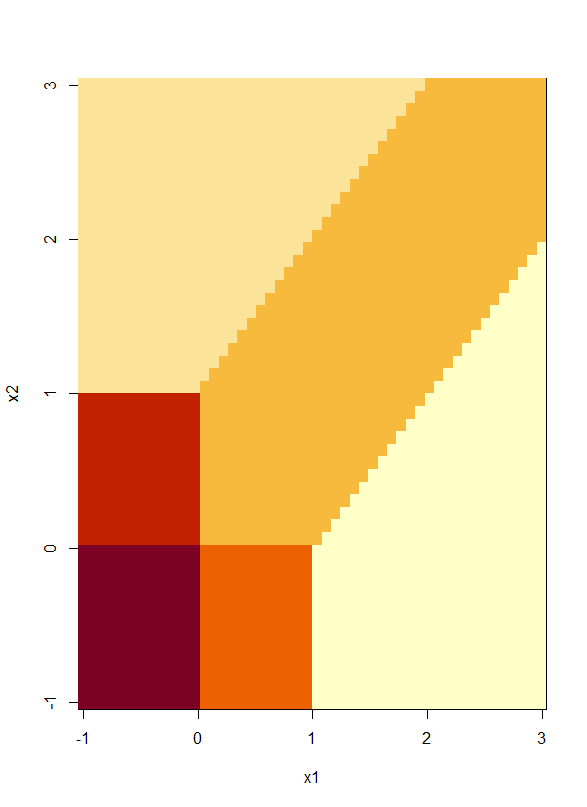
f:id:ryamada:20210318101247p:plain

x1 <- x2 <- seq(from=-1,to=3,length=50)
x1x2 <- expand.grid(x1,x2)

f1 <- function(x){1 + 2 * x[,1]}
f2 <- function(x){1 + 2 * x[,2]}
f3 <- function(x){2 + x[,1] + x[,2]}
f4 <- function(x){2 + x[,1]}
f5 <- function(x){2 + x[,2]}
f6 <- function(x){2}

fs <- list(f1,f2,f3,f4,f5,f6)

y <- matrix(0,length(x1x2[,1]),length(fs))
for(i in 1:length(fs)){
	tmp.f <- fs[[i]]
	for(j in 1:length(x1x2[,1])){
		y[j,i] <- tmp.f(x1x2[j,])
	}
}

minf <- apply(y,1,which.max)

image(x1,x2,matrix(minf,length(x1),length(x2)))

2021-03-08

Birkhoff polytopeと置換行列

Birkhoff polytope 置換

2021-03-07

Matrix Balancing、Sinkhornの定理

Matrix Balancing Sinkhornの定理二重確率行列置換行列 Birkhoff polytope

二重確率行列と言う行列がある
正方行列であって、すべての行和とすべての列和が１であり、かつ、行列の全成分が０以上(０より大)
二重確率行列を確率推行列とする確率推移では全要素値が均一状態に収束する
二重確率行列は、置換行列の線形和 $\sum_{i=1}^k p_i P_i$ と表せて、 $\sum_{i=1}^k p_i = 1; p_i >0$ となるという
もちろん、n!通りある、置換行列のすべてについて足し合わせてこの条件を満足することもできるが、実際には、n!よりもっと少ない置換行列の線形和で表せることが知られている
$\sum_{i=1}^k p_i P_i$ からわかるように、二重確率行列は置換行列が張る凸包の表面に相当する
二重確率行列の成分数は $n^2$ であるところ、置換行列の数はn!となっており、 $2^n << n!$ であるから、n!通りの置換行列を使わずとも、限定的な個数の置換行列の線形和で表せることになっている
さて。
任意の要素　正　なる正方行列　Aは $D A E$ と二つの正方行列でサンドイッチすることで、二重確率行列にすることができる。Sinkhornの定理

シンクホーンの定理 - Wikipedia

そして、D,Eは対角行列であって、対角成分は正だという
正成分の正方行列を二重確率行列にすることをmatrix balancingと言う
D,Eは単純な繰り返し計算により、近似的に求まることも知られている
そのアルゴリズムは複数、知られているが、以下の方法は、単純なアルゴリズムである
Aの成分 $a_{ij}$ は、i行の和とj列の和とを参考にして変化させたい値である
もし、i行の和だけで標準化するだけでよければ、i行の和で割れば、行和１を全行について達成できる
列の方だけを気にするなら、列和で割ればよい
今は行も列も整えたいので、 $a_{ij}$ 成分は、i行和とj列和の平方根の積で割ると、「良い感じ」
それを繰り返す

n <- 100
A <- matrix(runif(n^2),n,n)

As <- Ds <- Es <- list()
As[[1]] <- A
Ds[[1]] <- diag(rep(1,n))
Es[[1]] <- diag(rep(1,n))

# 繰り返し回数
n.iter <- 30

err <- rep(0,n.iter+1)
err[1] <- sum((apply(As[[1]],1,sum)-1)^2) + sum((apply(As[[1]],2,sum)-1)^2)

for(i in 1:n.iter){
	As[[i+1]] <- Ds[[i]] %*% As[[1]] %*% Es[[i]]
	tmp.r <- apply(As[[i+1]],1,sum) # 行和
	tmp.c <- apply(As[[i+1]],2,sum) # 列和
	tmp.d <- 1/sqrt(tmp.r) # 行和の平方根
	tmp.e <- 1/sqrt(tmp.c) # 列和の平方根
	Ds[[i+1]] <- diag(tmp.d) %*% Ds[[i]] # 行和に関して調整するのは対角行列を左からかけること
	Es[[i+1]] <- diag(tmp.e) %*% Es[[i]] # 列和に関して調整するのは対角行列を右からかけること
	# 行和、列和の１からのずれの二乗和を繰り返しごとに計算しておく
	err[i+1] <- sum((apply(As[[i+1]],1,sum)-1)^2) + sum((apply(As[[i+1]],2,sum)-1)^2)

}
# 結果の確認
apply(As[[n.iter+1]],1,sum)
apply(As[[n.iter+1]],2,sum)

plot(err)

# 関数化
my.sinkhorn.matbalance <- function(M,n.iter = 30){
	n <- length(M[,1])
	As <- Ds <- Es <- list()
	As[[1]] <- M
	Ds[[1]] <- diag(rep(1,n))
	Es[[1]] <- diag(rep(1,n))
	err <- rep(0,n.iter+1)
	err[1] <- sum((apply(As[[1]],1,sum)-1)^2) + sum((apply(As[[1]],2,sum)-1)^2)

	for(i in 1:n.iter){
		As[[i+1]] <- Ds[[i]] %*% As[[1]] %*% Es[[i]]
		tmp.r <- apply(As[[i+1]],1,sum) # 行和
		tmp.c <- apply(As[[i+1]],2,sum) # 列和
		tmp.d <- 1/sqrt(tmp.r) # 行和の平方根
		tmp.e <- 1/sqrt(tmp.c) # 列和の平方根
		Ds[[i+1]] <- diag(tmp.d) %*% Ds[[i]] # 行和に関して調整するのは対角行列を左からかけること
		Es[[i+1]] <- diag(tmp.e) %*% Es[[i]] # 列和に関して調整するのは対角行列を右からかけること
		# 行和、列和の１からのずれの二乗和を繰り返しごとに計算しておく
		err[i+1] <- sum((apply(As[[i+1]],1,sum)-1)^2) + sum((apply(As[[i+1]],2,sum)-1)^2)
	}
	return(list(double.st.mat=As[[n.iter+1]],D=Ds[[n.iter+1]],E=Es[[n.iter+1]],As=As,Ds=Ds,Es=Es,err=err))
}

M <- matrix(runif(n^2),n,n)

out <- my.sinkhorn.matbalance(M)
apply(out$double.st.mat,1,sum)
apply(out$double.st.mat,2,sum)

> apply(out$double.st.mat,1,sum)
  [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 [45] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 [89] 1 1 1 1 1 1 1 1 1 1 1 1
> apply(out$double.st.mat,2,sum)
  [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 [45] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 [89] 1 1 1 1 1 1 1 1 1 1 1 1

2021-03-03

Grassmannian-Pluckerの関係

グラスマニアン Plucker トレミーの定理 Ptolemy Grassmannian

2021-03-02

Ptolemy の定理とPlucker 座標、小行列式、flag minor、Grassmanian(2,n)

Ptolemyの定理 Plucker 座標 Plucker Flag minor

団代数をやっていると、Ptolemyの定理が出てくる
三角化の団代数では、円周上の４点ABCDについて、AC x BD = AB x CD + BC x ADという辺の長さの関係により、団変数の値の関係が論じられる
他方、Grassmanian(2,n) の団代数では、n角形の内部の三角化が論じられ、２行の行列Mについて、辺 i-j について、２ｘ２行列としてM[1:2,c(i,j)]を取り出し、その行列式の間に三角化における四角形の４辺と２つの対角線に相当する行列式の関係が持ち出される
もし、Grassmanian(2,n)のn角形を単位円周上に取れば、この行列式は、長さ１のベクトルに関する(x1y2 - x2y1)なる計算式で表されるが、これは $cos(t1)sin(t2)-cos(t2)sin(t1) = sin(t2-t1)$ となっていて、これは、２ベクトルが作る平行四辺形の面積に相当するが、これが、円周上の２点を結ぶ長さとも関連する、ということで、円周上４点の頂点間距離と行列式とが同じものを表していることが解る
そんな具合に、団代数のPtolemy定理は形を変えて現れる
ちなみに、行列式では $\sin{t1-t2}$ が現れ、トレミーの定理では $\sqrt{2 - 2\times \cos{t1-t2}}$ が辺・対角線の長さになっており、値自体は異なるが、団変異に伴う $\mu \theta = \alpha \times \gamma + \beta \times \delta$ の関係が、行列式でも直線の長さでも成立するというところがキモ

t1 <- runif(1)
t2 <- runif(1)
A <- c(cos(t1),sin(t1))
B <- c(cos(t2),sin(t2))
d <- sqrt(sum((A-B)^2))
d2 <- sin(t1-t2)

sqrt(2 - 2 * sqrt(1-d2^2))
d

ts <- sort(runif(4)*2*pi)

X <- rbind(cos(ts),sin(ts))

det(X[,1:2]) * det(X[,3:4]) + det(X[,2:3]) * det(X[,c(1,4)]) 
det(X[,c(1,3)]) * det(X[,c(2,4)])

L1 <- sqrt(sum((X[,1]-X[,2])^2))
L2 <- sqrt(sum((X[,2]-X[,3])^2))
L3 <- sqrt(sum((X[,3]-X[,4])^2))
L4 <- sqrt(sum((X[,4]-X[,1])^2))

L5 <- sqrt(sum((X[,1]-X[,3])^2))
L6 <- sqrt(sum((X[,2]-X[,4])^2))

L5 * L6

L1 * L3 + L2 * L4

上の例では、原点を中心とした単位円周上の４点の話
次に、２次元平面の任意の円周上の４点で、行列式と、辺・対角線の長さとの２つの演算が、変異に関して同様の等式を満足することを確かめる

ts <- sort(runif(4)) * 2 * pi
r <- runif(1) * 5
x0 <- rnorm(1) * 10
y0 <- rnorm(1) * 10


Vs <- r * rbind(cos(ts),sin(ts))

Vs[1,] <- Vs[1,] + x0
Vs[2,] <- Vs[2,] + y0

plot(t(Vs))

M12 <- Vs[,c(1,2)]
M23 <- Vs[,c(2,3)]
M34 <- Vs[,c(3,4)]
M14 <- Vs[,c(1,4)]

M13 <- Vs[,c(1,3)]
M24 <- Vs[,c(2,4)]

det(M13) * det(M24)
det(M12) * det(M34) + det(M23) * det(M14)

L12 <- sqrt(sum((M12[,1]-M12[,2])^2))
L23 <- sqrt(sum((M23[,1]-M23[,2])^2))
L34 <- sqrt(sum((M34[,1]-M34[,2])^2))
L14 <- sqrt(sum((M14[,1]-M14[,2])^2))

L13 <- sqrt(sum((M13[,1]-M13[,2])^2))
L24 <- sqrt(sum((M24[,1]-M24[,2])^2))

L13 * L24
L12 * L34 + L23 * L14

t <- sort(runif(4) * 2 * pi) * 10 # * 10 をしなければ、円周上に順番に並んだ点だが、それを大きく倍しても成り立つ…
sin(t[3]-t[1]) * sin(t[4]-t[2])
sin(t[2]-t[1]) * sin(t[4]-t[3]) + sin(t[3]-t[2]) * sin(t[4]-t[1])


M <- rbind(cos(t),sin(t))

d12 <- det(M[,1:2])
d13 <- det(M[,c(1,3)])
d14 <- det(M[,c(1,4)])
d23 <- det(M[,c(2,3)])
d24 <- det(M[,c(2,4)])
d34 <- det(M[,3:4])

d12 * d34 + d23 * d14

d13 * d24

ryamadaのコンピュータ・数学メモ

連分数と蛇グラフのパーフェクトマッチング数

Zonotope

トロピカル幾何、トロピカル曲面

Birkhoff polytopeと置換行列

Matrix Balancing、Sinkhornの定理

Grassmannian-Pluckerの関係

Ptolemy の定理とPlucker 座標、小行列式、flag minor、Grassmanian(2,n)